
【题目】将5个边长为1的正方形按照如图所示方式摆放,O1,O2,O3,O4,O5是正方形对角线的交点,那么阴影部分面积之和等于________.

 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣ ![]() ,﹣
,﹣ ![]() }=;若min{(x﹣1)2 , x2}=1,则x= .
}=;若min{(x﹣1)2 , x2}=1,则x= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题: ①若AC=AB,则DE=CE;
②若∠C=45°,记△CDE的面积为S1 , 四边形DABE的面积为S2 , 则S1=S2 ,
那么( )
A.①是真命题②是假命题
B.①是假命题②是真命题
C.①是假命题②是假命题
D.①是真命题②是真命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,AE⊥BC,CF⊥AD,垂足分别为E、F,AE、CF分别与BD相交于点G、H,联结AH、CG.
求证:四边形AGCH是平行四边形.
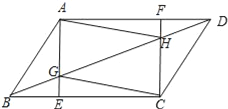
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
①AE=BF;②AE⊥BF;③sin∠BQP= ![]() ;④S四边形ECFG=2S△BGE .
;④S四边形ECFG=2S△BGE . 
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
, ![]() ,
, ![]() ,试说明:BE∥CF.
,试说明:BE∥CF.
完善下面的解答过程,并填写理由或数学式:
解:∵ ![]() (已知)
(已知)
∴AE∥ ( )
∴![]() ( )
( )
∵![]() (已知)
(已知)
∴![]() ( )
( )
∴DC∥AB( )
∴![]() ( )
( )
即![]()
∵![]() (已知)
(已知)
∴![]() ( )
( )
即![]()
∴BE∥CF( ) .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,点M是CE的中点,连接BM.
(1)如图①,点D在AB上,连接DM,并延长DM交BC于点N,可探究得出BD与BM的数量关系为______________;
(2)如图②,点D不在AB上,(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.
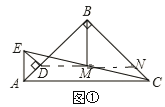

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com