
分析 先把括号内通分和除法运算化为乘法运算,再把分母因式分解,接着约分得到原式=-$\frac{1}{(a+b)^{2}}$,然后根据无理数的估算得到a=3,b=4,再把a和b的值代入原式=-$\frac{1}{(a+b)^{2}}$中运算即可.
解答 解:原式=[$\frac{a}{(a+b)(a-b)}$-$\frac{a-b}{(a+b)(a-b)}$]•$\frac{-(a-b)}{b(a+b)}$
=$\frac{b}{(a+b)(a-b)}$•$\frac{-(a-b)}{b(a+b)}$
=-$\frac{1}{(a+b)^{2}}$,
∵3<$\sqrt{13}$<4,
而a<$\sqrt{13}$<b,且a,b为连续正整数,
∴a=3,b=4,
∴原式=-$\frac{1}{(3+4)^{2}}$=-$\frac{1}{49}$.
点评 本题考查了分式的化简计算:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了无理数的估算.


科目:初中数学 来源: 题型:选择题
| A. | 10.3×10-5 | B. | 1.03×10-4 | C. | 0.103×10-3 | D. | 1.03×10-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
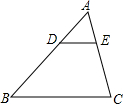 如图,在△ABC中,DE∥BC,若AD=1,DB=2,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,DE∥BC,若AD=1,DB=2,则$\frac{DE}{BC}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF.
如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com