
分析 由x+y=2,可得y=2-x,将x=1代入求出y=1,则满足条件的P点坐标为(1,1);将y=2-x代入-3x+2y=2a+7,整理得出x=-$\frac{2a+3}{5}$,则y=$\frac{2a+13}{5}$,由a是正数,即可判断P(x,y)所在的象限.
解答 解:∵x+y=2,
∴y=2-x,
将x=1代入,得y=1,
∴满足条件的P点坐标为(1,1);
将y=2-x代入-3x+2y=2a+7,
得-3x+2(2-x)=2a+7,
整理得x=-$\frac{2a+3}{5}$,
∴y=2-x=$\frac{2a+13}{5}$,
∵a是正数,
∴x<0,y>0,
∴P(x,y)在第二象限.
故答案为(1,1)(答案不唯一);二.
点评 本题考查了一次函数与二元一次方程,满足解析式的点就在函数的图象上,在函数的图象上的点,就一定满足函数解析式.同时考查了平面直角坐标系中各象限内点的坐标特征.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:选择题
| A. | 相等的圆心角所对的弧相等,所对的弦也相等 | |
| B. | 度数相等的弧是等弧 | |
| C. | 三点确定一个圆 | |
| D. | 圆周角是直角所对弦是直径 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
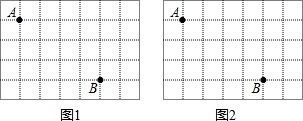
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
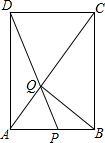 如图所示,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q,
如图所示,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com