
����Ŀ��Ϊ���˽�ij�о��꼶ѧ���������ɼ�(�ɼ���Ϊ����)�������ȡ�˲���ѧ���������ɼ����ֶ�(A��20.5��22.5��B��22.5��24.5��C��24.5��26.5��D��26.5��28.5��E��28.5��30.5)ͳ�����£������Ƴ�����ͼ��ʾ�IJ�������ͳ��ͼ��
�����ɼ�ͳ�Ʊ�
������ | Ƶ�� | Ƶ�� |
A | 12 | 0.05 |
B | 36 | a |
C | 84 | 0.35 |
D | b | 0.25 |
E | 48 | 0.20 |
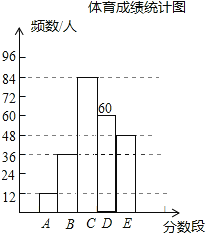
�����ɼ�ͳ��ͼ

���������ṩ����Ϣ������������⣺
(1)��ͳ�Ʊ��У�a��________��b��________������ͳ��ͼ����������
(2)С��˵�����������ݵ�����һ����C�У�������ΪС����˵����ȷ��__________(������ȷ������������)��
(3)���ɼ���27������(��27��)��Ϊ���㣬����н���48 000�����꼶ѧ���������ɼ�Ϊ�����ѧ��Լ�ж��٣�
���𰸡�(1) 0.15�� 60��(2) ��������3��21 600.
��������
��1������A����12�ˣ���Ӧ��Ƶ����0.05���������������Ȼ����ݰٷֱȵ��������a��b��ֵ��������ȫֱ��ͼ��
��2�����������Ķ��壬�Լ�ÿ���а���������ֻ���������������жϣ�
��3������������48000���Զ�Ӧ��Ƶ�ʼ�����⣮
��1���������������c=12��0.05=240���ˣ���
��a=![]() =0.15��b=240��0.25=60��
=0.15��b=240��0.25=60��
 ��
��
��2��C�����ݷ�Χ��24.5��26.5�����ڳɼ���Ϊ����������C��ijɼ�Ϊ25��26����ȻC��������࣬����25��26��������һ����࣮
�ʴ��ǣ�����
��3��48000����0.25+0.20��=21600���ˣ���
������48000�����꼶ѧ���������ɼ�Ϊ�����ѧ������Լ��21600�ˣ�


 ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
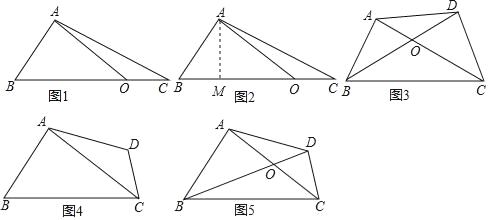
����Ŀ�����������ij��ҵ��˾���չ���ijС�����������̻����裬��Ҫ��һ���ı��εĿյأ���ͼ5���ı���ABCD�����ϲ�Ƥ�������������Զ��С���滮���ϸÿյص�������ݿ������ˣ��������������Խ���AC��BD�ij��ȷֱ�Ϊ20cm��30cm���нǡ�AOBΪ60��������������Щ���ݣ�������ҵ��Ա������յص������
������Ȼ��Ҫ���ı���ABCD�������ֻҪ�����ABD����BCD��Ҳ��������ABC����ACD�������������ӾͿ����ˣ�
����ģ�ͣ�������������ϼ������ε������
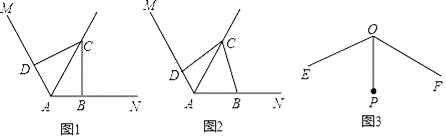
��ͼ1����ABC�У�OΪBC������һ�㣨����B��C�����غϣ�������OA��OA=a��BC=b����AOB=������ΪOA��BC���н�С�Ľǣ�������a��b������ʾ��ABC�������
�⣺��ͼ2����AM��BC�ڵ�M��
���AOMΪֱ�������Σ�
�֡ߡ�AOB=������sin��=![]() ��AM=OAsin��
��AM=OAsin��
���ABC�����=![]() BCAM=
BCAM=![]() BCOAsin��=
BCOAsin��=![]() absin����
absin����
��������������������ķ����������ҵ��˾�����⣮
��ͼ3���ı���ABCD�У�OΪ�Խ���AC��BD�Ľ��㣬��֪AC=20m��BD=30m����AOB=60�������ı���ABCD���������д�������������ͱ�Ҫ�Ľ����̣�
�½�ģ�ͣ����ı���ABCD�У�OΪ�Խ���AC��BD�Ľ��㣬��֪AC=a��BD=b����AOB=������ΪOA��BC���н�С�Ľǣ���ֱ��д���ı���ABCD�����=�� ����
ģ��Ӧ�ã���ͼ4���ı���ABCD�У�AB+CD=BC����ABC=��BCD=60������֪AC=a�����ı���ABCD�����Ϊ���٣������½�ģ�����еĽ��ۿ�ֱ�����ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ҳ�����ѧ����У���ֻ�������Ŀ�����ijУ�����꼶��ȤС������������˸�Уѧ���ҳ������������Ե����������������������²�������ͳ��ͼ��
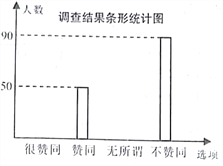
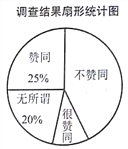
�����������Ϣ�������������
(1)��ν��ܵ���ļҳ�������Ϊ________�ˣ�
(2)������ͳ��ͼ������������ͬ������Ӧ������Բ�ĽǵĶ�����
(3)������ν��ܵ���ļҳ�����������һ���ҳ���ǡ�ó鵽������ν���ļҳ������Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
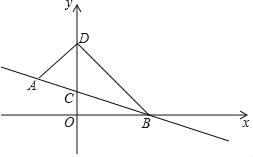
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB����A(��1��1)��B(2��0)����y���ڵ�C����D (0��n)�ڵ�C�Ϸ�������AD��BD��
(1)��ֱ��AB�Ĺ�ϵʽ��
(2)���ABD�������(�ú�n�Ĵ���ʽ��ʾ)
(3)��S��ABD��2ʱ��������ֱ��������DBP��ʹDB��DP�������P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�˶�Ь�������������ijУ40��Ů�����˶�Ь���룬������±���
Ь�ĺ��� | 35.5 | 36 | 36.5 | 37 | 37.5 |
���� | 4 | 6 | 16 | 12 | 2 |
���ڸþ�����Ҫ��200˫��������Ů�˶�Ь������ΪӦ�����������ȽϺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ijУΪ���˽�ѧ���İ�ȫ��ʶ����ȫУ��Χ�������ȡ����ѧ�������ʾ����飮���ݵ���������ѧ���İ�ȫ��ʶ�ֳɡ�����������һ�㡱������ǿ��������ǿ���ĸ���Σ������Ƴ����������в�������ͳ��ͼ����ͼ��ʾ��
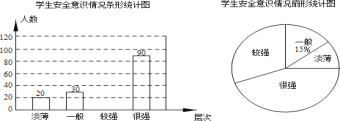
����������Ϣ������������⣺
��1����ε���һ����ȡ��______��ѧ����������ͳ��ͼ����������
��2������ͳ��ͼ�У�����ǿ�������ռԲ�ĽǵĴ�СΪ______�㣻
��3������У��3200��ѧ������Ҫ��ȫ��ʶΪ������������һ�㡱��ѧ��ǿ����ȫ���������ݵ��������������ȫУ��Ҫǿ����ȫ������ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ���Ķ�����IJ��ϣ��ٽ����������⣺������������ε���״��ͬ��������������������ƣ���ͼ1����ABC���DEF��״��ͬ����ơ�ABC���DEF���ƣ�������ABC�ס�DEF����ô�����˵�����������������أ����ǿ����á����Ƿֱ���ȵ����������ơ�����˵��������ѧ���Ա�ʾΪ��
��ͼ1���ڡ�ABC���DEF�У��ߡ�A=��D����B=��E�����ABC�ס�DEF��
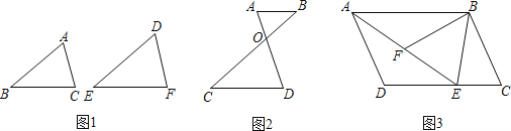
���������������������������⣺
��1������˵��������һ����Ϊ50��������������������ƣ�����һ����Ϊ100��������������������ƣ�����һ�������ȵ�����ֱ�����������ƣ��������ȱ����������ƣ�������ȷ����______������ţ���
��2����ͼ2����֪AB��CD��AD��BC�ཻ�ڵ�O����˵����ABO�ס�DCO��
��3����ͼ3����ƽ���ı���ABCD�У�E��DC��һ�㣬����AE��FΪAE��һ�㣬�ҡ�BFE=��C����֤����ABF�ס�EAD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������� ![]() ��x�ύ�ڵ�A����1��0������B��3��0������y�������ύ�ڵ�C.
��x�ύ�ڵ�A����1��0������B��3��0������y�������ύ�ڵ�C.
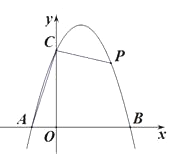
��1�������ߵĽ���ʽΪ________��
��2��PΪ��������һ�㣬����AC��PC������PCO=3��ACO����P������Ϊ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��MAN=120������C�ǡ�MAN��ƽ����AQ�ϵ�һ�����㣬��B��D�ֱ���AN��AM�ϣ�����BD��
�����֡�
��1����ͼ1������ABC=��ADC=90�������BCD=�� ��������CBD���� �������Σ�
��̽����
��2����ͼ2������ABC+��ADC=180�������ж���CBD����״����֤����Ľ��ۣ�
��Ӧ�á�
��3����ͼ3����֪��EOF=120����OPƽ�֡�EOF����OP=1������G��H�ֱ�������OE��OF�ϣ�����PGHΪ�ȱ������Σ�������������������PGH�ĸ���һ������ ������ֻ����ţ�
��2����3����4����4������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com