
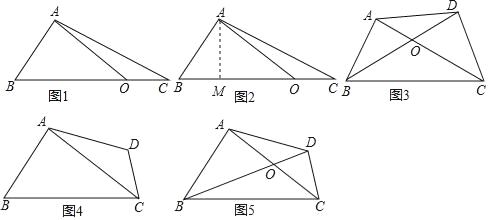
【题目】问题提出:某物业公司接收管理某小区后,准备进行绿化建设,现要将一块四边形的空地(如图5,四边形ABCD)铺上草皮,但由于年代久远,小区规划书上该空地的面积数据看不清了,仅仅留下两条对角线AC,BD的长度分别为20cm,30cm及夹角∠AOB为60°,你能利用这些数据,帮助物业人员求出这块空地的面积吗?
问题显然,要求四边形ABCD的面积,只要求出△ABD与△BCD(也可以是△ABC与△ACD)的面积,再相加就可以了.
建立模型:我们先来解决较简单的三角形的情况:
如图1,△ABC中,O为BC上任意一点(不与B,C两点重合),连接OA,OA=a,BC=b,∠AOB=α(α为OA与BC所夹较小的角),试用a,b,α表示△ABC的面积.
解:如图2,作AM⊥BC于点M,
∴△AOM为直角三角形.
又∵∠AOB=α,∴sinα=![]() 即AM=OAsinα
即AM=OAsinα
∴△ABC的面积=![]() BCAM=
BCAM=![]() BCOAsinα=
BCOAsinα=![]() absinα.
absinα.
问题解决:请你利用上面的方法,解决物业公司的问题.
如图3,四边形ABCD中,O为对角线AC,BD的交点,已知AC=20m,BD=30m,∠AOB=60°,求四边形ABCD的面积.(写出辅助线作法和必要的解答过程)
新建模型:若四边形ABCD中,O为对角线AC,BD的交点,已知AC=a,BD=b,∠AOB=α(α为OA与BC所夹较小的角),直接写出四边形ABCD的面积= .
模型应用:如图4,四边形ABCD中,AB+CD=BC,∠ABC=∠BCD=60°,已知AC=a,则四边形ABCD的面积为多少?(“新建模型”中的结论可直接利用)
【答案】问题解决:150![]() ;新建模型:
;新建模型: ![]() absinα, 模型应用:
absinα, 模型应用: ![]() a2
a2
【解析】
问题解决,如图5中,作AE⊥BD于E,CF⊥BD于F.根据S四边形ABCD=S△ABD+S△BCD计算即可;
新建模型,如图5中,作AE⊥BD于E,CF⊥BD于F.S四边形ABCD=S△ABD+S△BCD=![]() BDAE+
BDAE+![]() BDCF=
BDCF=![]() BD(AE+CF)=
BD(AE+CF)=![]() BD(OAsinα+OCsinα)=
BD(OAsinα+OCsinα)=![]() BDACsinα;
BDACsinα;
模型应用,如图4中,在CB上取CE=CD,连接DE,AE,BD.只要证明BD=AC,∠APB=60°即可;
解:问题解决,如图5中,作AE⊥BD于E,CF⊥BD于F.
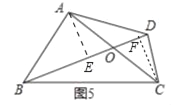
∵S四边形ABCD=S△ABD+S△BCD=![]() BDAE+
BDAE+![]() BDCF=
BDCF=![]() BD(AE+CF)=
BD(AE+CF)=![]() BD(OAsin60°+OCsin60°)=
BD(OAsin60°+OCsin60°)=![]() BDAC=150
BDAC=150![]() .
.
新建模型,如图5中,作AE⊥BD于E,CF⊥BD于F.
S四边形ABCD=S△ABD+S△BCD=![]() BDAE+
BDAE+![]() BDCF=
BDCF=![]() BD(AE+CF)=
BD(AE+CF)=![]() BD(OAsinα+OCsinα)=
BD(OAsinα+OCsinα)=![]() BDACsinα=
BDACsinα=![]() absinα,
absinα,
故答案为![]() absinα.
absinα.
模型应用,如图4中,在CB上取CE=CD,连接DE,AE,BD.
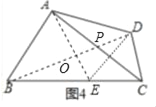
∵AB+DC=BC,
∴AB=BE,
∵∠ABC=∠BCD=60°,
∴△ABE与△CDE均为等边三角形,
∴AE=BE,DE=CE,
∴∠AEB=∠CED=60°,
∴∠BED=∠AEC=120°,
在△BED与△AEC中,
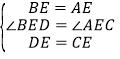 ,
,
∴△BED≌△AEC(SAS),
∴AC=BD,∠EAC=∠EBD,
∵∠AOP=∠BOE,
∴∠APO=∠AEB=60°,
∴S四边形ABCD=![]() aasin60°=
aasin60°=![]() a2.
a2.


科目:初中数学 来源: 题型:
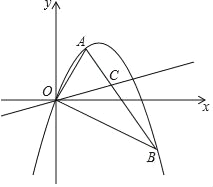
【题目】如图,抛物线y=ax2+bx经过△OAB的三个顶点,其中点A(1,![]() ),点B(3,﹣
),点B(3,﹣![]() ),O为坐标原点.
),O为坐标原点.
(1)求这条抛物线所对应的函数表达式;
(2)若P(4,m),Q(t,n)为该抛物线上的两点,且n<m,求t的取值范围;
(3)若C为线段AB上的一个动点,当点A,点B到直线OC的距离之和最大时,求∠BOC的大小及点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
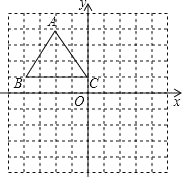
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣2,4),B(﹣4,1),C(0,1).
(1)画出与△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;
(2)画出以C1为旋转中心,将△A1B1C1逆时针旋转90°后的△A2B2C2;
(3)尺规作图:连接A1A2,在C1A2边上求作一点P,使得点P到A1A2的距离等于PC1的长(保留作图痕迹,不写作法);
(4)请直接写出∠C1A1P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,晚上小亮在广场上乘凉,图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
请你再图中画出小亮在照明灯P照射下的影子BC;
如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向![]() 海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
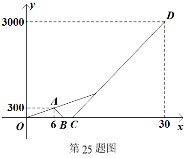
为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆.已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与出发的时间x(分钟)的函数图象,根据图象解答下列问题:
⑴小亮在家停留了 分钟.
⑵求小亮骑单车从家出发去图书馆时距家的路程y(米)与出发时间x(分钟)之间的函数关系式.
⑶若小亮和姐姐到图书馆的实际时间为m分钟,原计划步行到达图书馆的时间为n分钟,则n-m= 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计如下,而且制成了如图所示的不完整的统计图.
体育成绩统计表
分数段 | 频数 | 频率 |
A | 12 | 0.05 |
B | 36 | a |
C | 84 | 0.35 |
D | b | 0.25 |
E | 48 | 0.20 |
体育成绩统计图

根据上面提供的信息,解答下列问题:
(1)在统计表中,a=________,b=________,并将统计图补充完整;
(2)小明说:“这组数据的众数一定在C中.”你认为小明的说法正确吗?__________(填“正确”或“错误”).
(3)若成绩在27分以上(含27分)定为优秀,则该市今年48 000名九年级学生中体育成绩为优秀的学生约有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com