
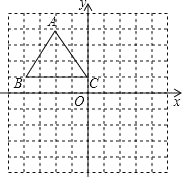
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣2,4),B(﹣4,1),C(0,1).
(1)画出与△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;
(2)画出以C1为旋转中心,将△A1B1C1逆时针旋转90°后的△A2B2C2;
(3)尺规作图:连接A1A2,在C1A2边上求作一点P,使得点P到A1A2的距离等于PC1的长(保留作图痕迹,不写作法);
(4)请直接写出∠C1A1P的度数.
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
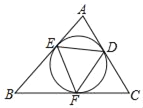
【题目】如图,△ABC的内切圆与三边分别相切于点D、E、F,则下列等式:
①∠EDF=∠B;
②2∠EDF=∠A+∠C;
③2∠A=∠FED+∠EDF;
④∠AED+∠BFE+∠CDF=180°,其中成立的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A.5![]() B.25C.10
B.25C.10![]() +5D.35
+5D.35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
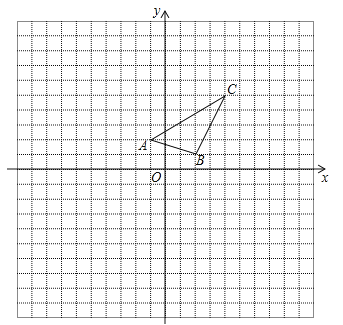
【题目】如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)画出△ABC关于x对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
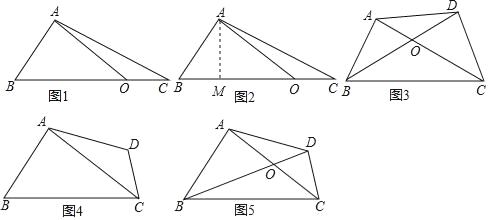
【题目】问题提出:某物业公司接收管理某小区后,准备进行绿化建设,现要将一块四边形的空地(如图5,四边形ABCD)铺上草皮,但由于年代久远,小区规划书上该空地的面积数据看不清了,仅仅留下两条对角线AC,BD的长度分别为20cm,30cm及夹角∠AOB为60°,你能利用这些数据,帮助物业人员求出这块空地的面积吗?
问题显然,要求四边形ABCD的面积,只要求出△ABD与△BCD(也可以是△ABC与△ACD)的面积,再相加就可以了.
建立模型:我们先来解决较简单的三角形的情况:
如图1,△ABC中,O为BC上任意一点(不与B,C两点重合),连接OA,OA=a,BC=b,∠AOB=α(α为OA与BC所夹较小的角),试用a,b,α表示△ABC的面积.
解:如图2,作AM⊥BC于点M,
∴△AOM为直角三角形.
又∵∠AOB=α,∴sinα=![]() 即AM=OAsinα
即AM=OAsinα
∴△ABC的面积=![]() BCAM=
BCAM=![]() BCOAsinα=
BCOAsinα=![]() absinα.
absinα.
问题解决:请你利用上面的方法,解决物业公司的问题.
如图3,四边形ABCD中,O为对角线AC,BD的交点,已知AC=20m,BD=30m,∠AOB=60°,求四边形ABCD的面积.(写出辅助线作法和必要的解答过程)
新建模型:若四边形ABCD中,O为对角线AC,BD的交点,已知AC=a,BD=b,∠AOB=α(α为OA与BC所夹较小的角),直接写出四边形ABCD的面积= .
模型应用:如图4,四边形ABCD中,AB+CD=BC,∠ABC=∠BCD=60°,已知AC=a,则四边形ABCD的面积为多少?(“新建模型”中的结论可直接利用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解家长对“学生在校带手机”现象的看法,某校“九年级兴趣小组”随机调查了该校学生家长若干名,并对调查结果进行整理,绘制如下不完整的统计图:
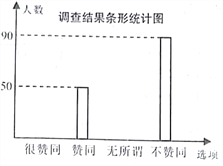
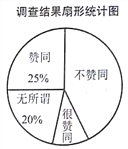
请根据以上信息,解答下列问题
(1)这次接受调查的家长总人数为________人;
(2)在扇形统计图中,求“很赞同”所对应的扇形圆心角的度数;
(3)若在这次接受调查的家长中,随机抽出一名家长,恰好抽到“无所谓”的家长概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com