Question

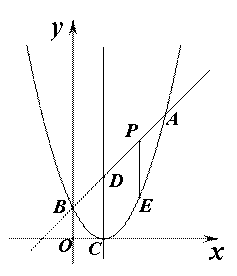
如图，已知二次函数图象的顶点坐标为C（1，0），直线y=x+m与该二次函数的图象交于A、B两点，其中A点的坐标为（3，4），B点在y轴上。

(1).求m的值及这个二次函数的解析式；

(2).点P为线段AB上的一个动点（点P与A、B不重合），过P点作x轴的垂线与这个二次函数的图象交于E点，设线段PE的长为h，点P的横坐标为x 。

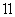求h与x之间的函数关系式，并写出自变量的取值范围；

点D为直线AB与这个二次函数图象对称轴的交点，在线段AB上是否存在一点P，使得四边形DCEP是平行四边形？若存在，请求出此时P点的坐标；若不存在，请说明理由。

                                   

Answer 1

解：(1)把A(3，4)代入y=x+m得

4=3+m ，∴m=1

由抛物线的顶点为C（3,4）可设函数解析式为y=a(x—1)² ,把A（3,4）代入得，

4=a(3—1)²   ∴ a=1

∴ 二次函数的解析式为y=(x—1)²

.(2) 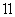由(1)知直线AB的解析式为y=x+1

∵ 点P在直线AB上，且点P的横坐标为x，

∴点P的纵坐标y_P=x+1 ，

由PE⊥x轴知点E的横坐标为x ，

∵ 点E在抛物线上，∴ 点E的纵坐标y_E=(x—1)²

∴ PE=y_P—y_E=（x+1）—(x—1)²= —x²+3x

即 h= —x²+3x   (0<x<3)  存在符合条件的点P，理由如下

当PE=DC时，∵ PE∥DC，且PE=DC，

∴ 四边形DCEP是平行四边形，

函数y=x+1当x=1时，y=2 ，

∴ D（1,2）∴ DC=2 ，∴PE=2

即  —x²+3x=2    解得x₁=1(舍去)  ,x₂=2

当x=2时，y_P=x+1=3   

∴ 点P的坐标为（2,3）