
【题目】如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.

(1)求证:△ABE≌△DBE;
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
【答案】(1)详见解析;(2)65°.
【解析】
(1)由角平分线定义得出∠ABE=∠DBE,由SAS证明△ABE≌△DBE即可;
(2)由三角形内角和定理得出∠ABC=30°,由角平分线定义得出∠ABE=∠DBE![]() ∠ABC=15°,在△ABE中,由三角形内角和定理即可得出答案.
∠ABC=15°,在△ABE中,由三角形内角和定理即可得出答案.
(1)证明:∵BE平分∠ABC,
∴∠ABE=∠DBE,
在△ABE和△DBE中,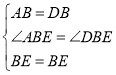 ,
,
∴△ABE≌△DBE(SAS);
(2)解:∵∠A=100°,∠C=50°,
∴∠ABC=30°,
∵BE平分∠ABC,
∴∠ABE=∠DBE![]() ∠ABC=15°,
∠ABC=15°,
在△ABE中,∠AEB=180°﹣∠A﹣∠ABE=180°﹣100°﹣15°=65°.


科目:初中数学 来源: 题型:
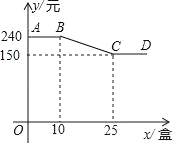
【题目】中秋节前夕,某公司的李会计受公司委派去超市购买若干盒美心月饼,超市给出了该种月饼不同购买数量的价格优惠,如图,折线ABCD表示购买这种月饼每盒的价格y(元)与盒数x(盒)之间的函数关系.
(1)当购买这种月饼盒数不超过10盒时,一盒月饼的价格为 元;
(2)求出当10<x<25时,y与x之间的函数关系式;
(3)当时李会计支付了3600元购买这种月饼,那么李会计买了多少盒这种月饼?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC按逆时针方向绕点B旋转90°得到线段BE,连接AE.若AB=2,DC=4,则△ABE的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,A(1,-1)、B(l,-3)、C(4,-3).
(1)△![]()
![]()
![]() 是△ABC关于x轴的对称图形,则点A的对称点
是△ABC关于x轴的对称图形,则点A的对称点![]() 的坐标是_______;
的坐标是_______;
(2)将△ABC绕点(0,1)逆时针旋转90 °得到△A![]() B
B![]() C
C![]() ,则B点的对应点B
,则B点的对应点B![]() 的坐标是____;
的坐标是____;
(3)△![]()
![]()
![]() 与△A
与△A![]() B
B![]() C
C![]() 是否关于某条直线成轴对称?若成轴对称,则对称轴的解析式是_________________
是否关于某条直线成轴对称?若成轴对称,则对称轴的解析式是_________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,四边形ABCD中,AB=7,BC=3,∠ABC=∠ACD=∠ADC=45°,求BD的长;
(2)如图2,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).

(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,∠A = ∠D,试说明 AC∥DE 成立的理由.

下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整。
解:∵ AB ∥ CD (已知)
∴ ∠A = (两直线平行,内错角相等)
又∵ ∠A = ∠D( )
∴ ∠ = ∠ (等量代换)
∴ AC ∥ DE ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某驻村扶贫小组为解决当地贫困问题,带领大家致富.经过调查研究,他们决定利用当地生产的甲乙两种原料开发A,B两种商品,为科学决策,他们试生产A、B两种商品100千克进行深入研究,已知现有甲种原料293千克,乙种原料314千克,生产1千克A商品,1千克B商品所需要的甲、乙两种原料及生产成本如下表所示.
甲种原料(单位:千克) | 乙种原料(单位:千克) | 生产成本(单位:元) | |
A商品 | 3 | 2 | 120 |
B商品 | 2.5 | 3.5 | 200 |
设生产A种商品x千克,生产A、B两种商品共100千克的总成本为y元,根据上述信息,解答下列问题:
(1)求y与x的函数解析式(也称关系式),并直接写出x的取值范围;
(2)x取何值时,总成本y最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com