
【题目】如图,在△ABC中,A(1,-1)、B(l,-3)、C(4,-3).
(1)△![]()
![]()
![]() 是△ABC关于x轴的对称图形,则点A的对称点
是△ABC关于x轴的对称图形,则点A的对称点![]() 的坐标是_______;
的坐标是_______;
(2)将△ABC绕点(0,1)逆时针旋转90 °得到△A![]() B
B![]() C
C![]() ,则B点的对应点B
,则B点的对应点B![]() 的坐标是____;
的坐标是____;
(3)△![]()
![]()
![]() 与△A
与△A![]() B
B![]() C
C![]() 是否关于某条直线成轴对称?若成轴对称,则对称轴的解析式是_________________
是否关于某条直线成轴对称?若成轴对称,则对称轴的解析式是_________________

【答案】(1) (-1,-1);(2) (4,2);(3) y=-x+1.
【解析】
(1)根据轴对称的性质及关于y轴对称的点的坐标特征解答即可.
(2)利用网格,将图形旋转90°,即可得到B2的坐标.
(3)连接△A1B1C1与△A2B2C2的对应点,对应点连线的垂直平分线即为所求直线.
(1)由图可知,A的对应点A1的坐标为(-1,-1).
故答案为:(-1,-1).
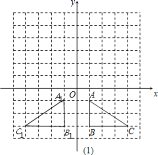
(2)由图可知,![]() 的坐标为(4,2);
的坐标为(4,2);
故答案为:(4,2).

(3)由图可见,直线过(0,1)和(1,0),
设函数解析式为y=kx+b,将(0,1)和(1,0)分别代入解析式得,
![]() ,
,
解得![]() ,
,
故的函数解析式为y=-x+1.
故答案为:y=-x+1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】把抛物线y=ax![]() +bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x
+bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x![]() -3x+5,则a+b+c=__________。
-3x+5,则a+b+c=__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上, 老师要求同学们利用三角板画两条平行线.老师说苗苗和小华两位同学画法都是正确的,两位同学的画法如下:
苗苗的画法:

①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b//a.
小华的画法:

①将含30°角三角尺的最长边与直线a重合,用虚线做出一条最短边所在直线;
②再次将含30°角三角尺的最短边与虚线重合,画出最长边所在直线b,则b//a.
请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种,并写出这种画图的依据.
答:我喜欢__________同学的画法,画图的依据是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据PM2.5检测网的空气质量新标准,从德州市2013年全年每天的PM2.5日均值标准值(单位:微克/立方米)监测数据中随机地抽取25天的数据作为样本,并根据检测数据制作了尚不完整的频数分布表和条形图:
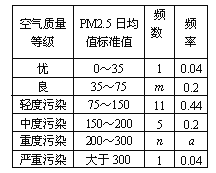
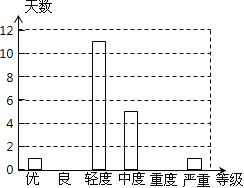
(1)求出表中m,n,a的值,并将条形图补充完整;
(2)以这25天的PM2.5日均值来估计该年的空气质量情况,估计该年(365天)大约有多少天的空气质量达到优或良;
(3)请你结合图表评价一下我市的空气质量情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个边长都为2的正方形A BCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕D点旋转,那么它们重叠部分的面积为( )

A. 4 B. 2 C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A=36°,将△ABC绕平面中的某一点D按顺时针方向旋转一定角度得到△![]()
![]()
![]() .
.
(1)若旋转后的图形如图所示,请在图中用尺规作出点D,请保留作图痕迹,不要求写作法;
(2)若将△ABC按顺时针方向旋转到△![]()
![]()
![]() 的旋转角度为
的旋转角度为![]() (0°<
(0°<![]() <180°),且AC⊥
<180°),且AC⊥![]()
![]() ,直接写出旋转角度
,直接写出旋转角度![]() 的值为_____.
的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.

(1)求证:△ABE≌△DBE;
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的题目及分析过程.已知:如图点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]()



原图 ① ②
说明:![]()
说明两个角相等,常用的方法是应用全等三角形或等腰三角形的性质.观察本题中说明的两个角,它们既不在同一个三角形中,而且们所在两个三角形也不全等.因此,要说明![]() ,必须添加适当的辅助线,构造全等三角形或等腰三角形,现在提供两种添加辅加线的方法如下:
,必须添加适当的辅助线,构造全等三角形或等腰三角形,现在提供两种添加辅加线的方法如下:
如图①过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
如图②延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)请从以上两种辅助线中选择一种完成上题的说理过程.
(2)在解决上述问题的过程中,你用到了哪种数学思想?请写出一个._______________.
(3)反思应用:

如图,点![]() 是
是![]() 的中点,
的中点,![]() 于点
于点![]() .
.
请类比(1)中解决问题的思想方法,添加适当的辅助线,判断线段![]() 与
与![]() 之间的大小关系,并说明理由.
之间的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50°

(1)求证:①AC=BD;②∠APB=50°;
(2)如图②,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=α,则AC与BD间的等量关系为 ,∠APB的大小为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com