
【题目】已知:如图①,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50°

(1)求证:①AC=BD;②∠APB=50°;
(2)如图②,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=α,则AC与BD间的等量关系为 ,∠APB的大小为
【答案】(1)见解析;(2)AC=BD,α.
【解析】
试题分析:(1)根据∠AOB=∠COD=50°求出∠AOC=∠BOD,根据SAS推出△AOC≌△BOD,根据全等三角形的性质得出AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,推出∠APB=∠AOB即可.
(2)根据∠AOB=∠COD=50°求出∠AOC=∠BOD,根据SAS推出△AOC≌△BOD,根据全等三角形的性质得出AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,推出∠APB=∠AOB即可.
证明:(1)∵∠AOB=∠COD=50°,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
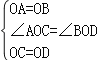
∴△AOC≌△BOD,
∴AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,
∴∠APB=∠AOB=50°.
(2)解:AC=BD,∠APB=α,
理由是:)∵∠AOB=∠COD=50°,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
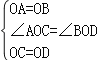
∴△AOC≌△BOD,
∴AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,
∴∠APB=∠AOB=α,
故答案为:AC=BD,α.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如图,小红做了一个实验,将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F′的位置,所转过的度数是( ) 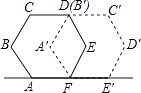
A.60°
B.72°
C.108°
D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
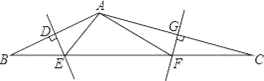
【题目】如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F.
(1)若△AEF的周长为10cm,则BC的长为______cm.
(2)若∠EAF=100°,则∠BAC______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格图中小方格都是边长为1个单位长度的小正方形,已知三角形ABC的三个顶点都在网格的格点上,按要求完成下列各小题.
(1)请在图中画出将三角形ABC先向上平移1个单位长度,再向右平移3个单位长度后的图形,即三角形A′B′C′,并指出图中相等的线段;
(2)在(1)的基础上,A′B′,B′C′分别与AC交于点E,F.若∠A=50°,∠C′=51°,分别求出∠A′EF与∠B′FC的度数.
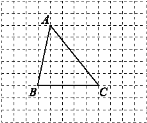
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为⊙O外一点,PA、PB为⊙O的切线,A、B为切点,AC为⊙O的直径,PO交于⊙O于点E. 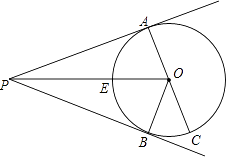
(1)试判断∠APB与∠BAC的数量关系;
(2)若⊙O的半径为4,P是⊙O外一动点,是否存在点P,使四边形PAOB为正方形?若存在,请求出PO的长,并判断点P的个数及其满足的条件;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的顶点上. 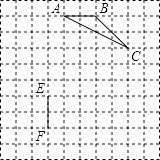
(1)填空:tanA= , AC=(结果保留根号);
(2)请你在图中找出一点D(仅一个点即可),连接DE、DF,使以D、E、F为顶点的三角形与△ABC全等,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机上网已经成为当今年轻人时尚的网络生活,某网络公司看中了这种商机,推出了两种手机上网的计费方式:方式A以每分钟0.1元的价格按上网时间计费;方式B除收月基费20元外,再以每分钟0.06元的价格按上网时间计费.假设某客户月手机上网的时间为x分钟,上网费用为y元. 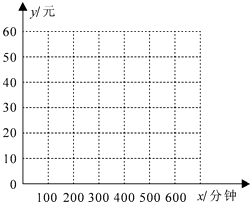
(1)分别写出该客户按A、B两种方式的上网费y(元)与每月上网时间x(分钟)的函数关系式,并在右图的坐标系中画出这两个函数的图象;
(2)如何选择计费方式能使该客户上网费用更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市正在进行商业街改造,商业街起点在古民居P的南偏西60°方向上的A处,现已改造至古民居P南偏西30°方向上的B处,A与B相距150m,且B在A的正东方向.为不破坏古民居的风貌,按照有关规定,在古民居周围100m以内不得修建现代化商业街.若工程队继续向正东方向修建200m商业街到C处,则对于从B到C的商业街改造是否违反有关规定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图与计算
(1)已知:![]() .
.
求作:在图2中,以OA为一边,在∠AOB的内部作.∠AOC=![]() (要求:直尺和圆规作图,不写作法,保留图痕迹.)
(要求:直尺和圆规作图,不写作法,保留图痕迹.)

(2)过点O分别引射线OA、OB、OC,且∠AOB=65°,∠BOC=30°,求∠AOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com