
【题目】如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F.
(1)若△AEF的周长为10cm,则BC的长为______cm.
(2)若∠EAF=100°,则∠BAC______.
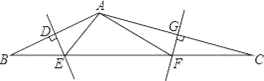
【答案】 10 140°
【解析】(1)∵ED、FG分别是AB、AC的垂直平分线,
∴AE=BE,AF=CF,
∵△AEF的周长为10cm,
∴AC=10cm;
(2)∵∠EAF=100°,
∴∠AEF+∠AFE=80°,
∵ED、FG分别是AB、AC的垂直平分线,
∴EA=EB,FA=FC,
∴∠AEF=2∠EAB,∠AFE=2∠CAF,
∴∠BAC=∠EAF+∠EAB+∠FAC=100°+∠EAB+∠CAF=100°+12(∠AEF+∠AFE)=140°.
故答案为:10,140°.
点睛: 本题主要考查了线段的垂直平分线的性质等几何知识,线段的垂直平分线上的点到线段的两个端点的距离相等,以及外角的性质,难度适中.


科目:初中数学 来源: 题型:
【题目】已知一个由50个偶数排成的数阵,请你观察框内的四个数之间的关系并解答下列问题:在数阵中任意作一个类似图中的框. 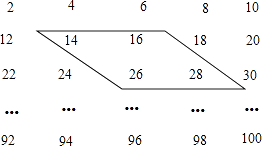
(1)设框内左上角的数为x,那么其他三个数分别是: , ,
(2)如果框内四个数的和是172,这四个数分别是什么?
(3)框内四个数的和有没有可能是322,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0. ![]()
(1)求A、B两点的坐标;
(2)点C在数轴上对应的数为x,且x是方程2x+1= ![]() x﹣8的解
x﹣8的解
①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?求出点P对应的数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若把一次函数y=2x﹣3,向下平移3个单位长度,得到图象解析式是( )
A. y=2x B. y=2x﹣6 C. y=5x﹣3 D. y=﹣x﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
①射线 AB 和射线 BA 是同一条射线;②若 AB=BC,则点B为线段AC的中点;③同角的补角相等;④线段AB和线段BA 是同一条线段
A. ①② B. ②③ C. ②④ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com