
【题目】综合与探究:在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .过动点
.过动点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,直线
,直线![]() 与抛物线相交于点
与抛物线相交于点![]() ,
,![]() .线段
.线段![]() 的中点为
的中点为![]() .
.
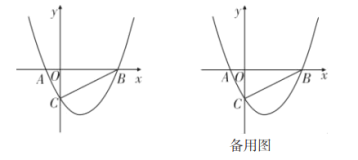
(1)求抛物线的表达式;
(2)若![]() ,且点
,且点![]() 到
到![]() 轴的距离正好等于
轴的距离正好等于![]() 时,求
时,求![]() 的值;
的值;
(3)直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 是以
是以![]() 为直角边的等腰直角三角形?若存在,直接写出
为直角边的等腰直角三角形?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 的值为
的值为![]() ;(3)存在,
;(3)存在,![]() 的值为4或2
的值为4或2
【解析】
(1)把![]() 和点
和点![]() 坐标分别代入表达式求出即可;
坐标分别代入表达式求出即可;
(2)因为线段![]() 的中点为
的中点为![]() ,所以点H在抛物线的对称轴上,进而得出点H的坐标,可以得出E、F点的坐标,把其坐标代入表达式解出m值即可;
,所以点H在抛物线的对称轴上,进而得出点H的坐标,可以得出E、F点的坐标,把其坐标代入表达式解出m值即可;
(3)使得![]() 是以
是以![]() 为直角边的等腰直角三角形重点明白有几种情况,求解时利用全等三角形知识点易得m的值.
为直角边的等腰直角三角形重点明白有几种情况,求解时利用全等三角形知识点易得m的值.
(1)抛物线![]() 经过点
经过点![]() 和点
和点![]() ,
,
∴![]() ,
,
解得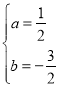 .
.
∴抛物线的表达式为![]() .
.
(2)∵![]() .
.
∴抛物线的对称轴为直线![]() .
.
∴点![]() 的坐标为
的坐标为![]() .
.
∴点![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() .
.
∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() .
.
解得![]() 或
或![]() (不合题意,舍去).
(不合题意,舍去).
∴![]() 的值为
的值为![]() .
.
(3)①当点C为等腰直角三角形的顶点时,如下图所示:
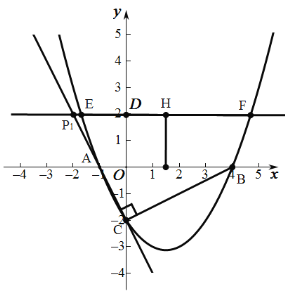
∵![]()
∴![]()
在![]() 和
和![]() 中
中
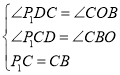
∴![]()
∴![]()
∴![]()
②当点B为等腰直角三角形的顶点时,如下图所示:
过点![]() 作
作![]() 轴垂足为
轴垂足为![]()
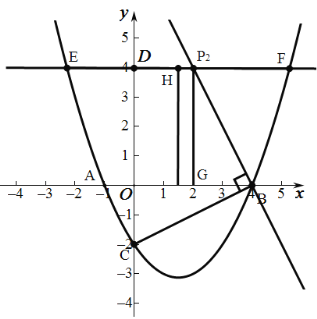
同理可得![]()
∴![]()
∴![]()
综上所述:![]() 的值为4或2.
的值为4或2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F.
(1)如图1,当点E在线段AC上时,求证:△DEC∽△DFB.
(2)当点E在线段AC的延长线上时,(1)中的结论是否仍然成立?若成立,请结合图2给出证明;若不成立,请说明理由;
(3)若AC=![]() ,BC=2
,BC=2![]() ,DF=4
,DF=4![]() ,请直接写出CE的长.
,请直接写出CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形![]() 的边长为2,
的边长为2,![]() =60°,对角线
=60°,对角线![]() ,
,![]() 相交于点O.以点O为坐标原点,分别以
相交于点O.以点O为坐标原点,分别以![]() ,
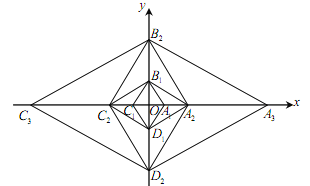
,![]() 所在直线为x轴、y轴,建立如图所示的直角坐标系.以
所在直线为x轴、y轴,建立如图所示的直角坐标系.以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,,按此规律继续作下去,在x轴的正半轴上得到点
,,按此规律继续作下去,在x轴的正半轴上得到点![]() ,
,![]() ,
,![]() ,......,
,......,![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
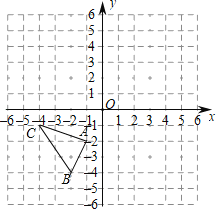
【题目】如图,平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)在平面直角坐标系中画出与△ABC关于点P(1,0)成中心对称的△A'B'C',并分别写出点A',B',C'的坐标;
(2)如果点M(a,b)是△ABC边上(不与A,B,C重合)任意一点,请写出在△A'B'C'上与点M对应的点M'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
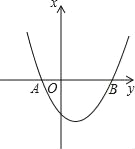
【题目】抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式.
(2)一动点P在(1)中抛物线上滑动且满足S△ABP=10,求此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
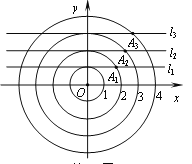
【题目】如图,在平面直角坐标系中,点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点;点A2是以原点O为圆心,半径为3的圆与过点(0,2)且平行于x轴的直线l2的一个交点;……按照这样的规律进行下去,点An的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知△ABC,∠ABC=90°,顶点A在第一象限,顶点B、C在x轴的正半轴上(C在B的右侧),
中,已知△ABC,∠ABC=90°,顶点A在第一象限,顶点B、C在x轴的正半轴上(C在B的右侧),![]() ,△ADC与△ABC关于AC所在的直线对称.
,△ADC与△ABC关于AC所在的直线对称.
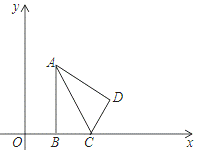
(1)当OB=2时,求点D的坐标.
(2)若点![]() 和点
和点![]() 在同一个反比例函数图象上,求
在同一个反比例函数图象上,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转一定角度后,点
顺时针旋转一定角度后,点![]() 的对应点恰好与点
的对应点恰好与点![]() 重合,得到
重合,得到![]() .
.
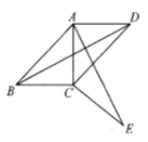
(1)请求出旋转角的度数;
(2)请判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若![]() ,
,![]() ,试求出四边形
,试求出四边形![]() 的对角线
的对角线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西汾酒,又称“杏花村酒”.酿造汾酒是选用晋中平原的“一把抓高粱”为原料.汾阳县某村民合作社2016年种植“一把抓高粱”100亩,2018年该合作社扩大了“一把抓高梁”的种植面积,共种植144亩.
(1)求该合作社这两年种植“一把抓高梁”亩数的平均增长率;
(2)某粮店销售“一把抓高粱”售价为13元/斤,每天可售出30斤,每斤的盈利是1.5元.为了减少库存,粮店决定搞促销活动.在销售中发现:售价每降价0.1元,则可多售出2斤.若该粮店某天销售“一把抓高梁”的盈利为40元,则该店当天销售单价降低了多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com