
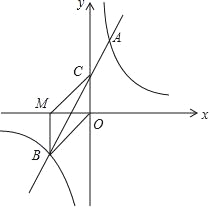
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.
【答案】(1)y=2x+2;(2)4
【解析】试题分析:(1)根据题意可以求得点B的坐标,从而可以求得反比例函数的解析式,进而求得点A的坐标,从而可以求得一次函数的解析式;
(2)根据(1)中的函数解析式可以求得点C,点M、点B、点O的坐标,从而可以求得四边形MBOC的面积.
试题解析:(1)由题意可得,BM=OM,OB=![]() ,∴BM=OM=2,∴点B的坐标为(﹣2,﹣2),设反比例函数的解析式为
,∴BM=OM=2,∴点B的坐标为(﹣2,﹣2),设反比例函数的解析式为![]() ,则﹣2=
,则﹣2=![]() ,得k=4,∴反比例函数的解析式为
,得k=4,∴反比例函数的解析式为![]() ,∵点A的纵坐标是4,∴4=
,∵点A的纵坐标是4,∴4=![]() ,得x=1,∴点A的坐标为(1,4),∵一次函数y=mx+n(m≠0)的图象过点A(1,4)、点B(﹣2,﹣2),∴
,得x=1,∴点A的坐标为(1,4),∵一次函数y=mx+n(m≠0)的图象过点A(1,4)、点B(﹣2,﹣2),∴![]() ,得:
,得:![]() ,即一次函数的解析式为y=2x+2;
,即一次函数的解析式为y=2x+2;
(2)∵y=2x+2与y轴交与点C,∴点C的坐标为(0,2),∵点B(﹣2,﹣2),点M(﹣2,0),点O(0,0),∴OM=2,OC=2,MB=2,∴四边形MBOC的面积是:![]() OMON+
OMON+![]() OMMB =
OMMB =![]() ×2×2+
×2×2+![]() ×2×2=4.
×2×2=4.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
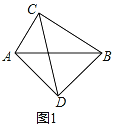
【题目】问题背景:如图(1)在四边形ABCD中,∠ACB=∠ADB=90°,AD=BD,探究线段AC、BC、CD之间的数量关系.小明探究此问题的思路是:将△BCD绕点D逆时针旋转90°到△AED处,点B、C分别落在点A、E处(如图(2)),易证点C、A、E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=![]() CD.
CD.
简单应用:
(1)在图(1)中,若AC=![]() ,BC=2
,BC=2![]() ,求CD的长;
,求CD的长;
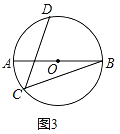
(2)如图(3)AB是⊙O的直径,点C、D在⊙O上,AD=BD,若AB=13,BC=12,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
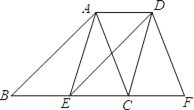
【题目】如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
(1)求证:△ABC≌△DEF;
(2)求证:四边形ACFD为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生小明、小华为了解本校八年级学生每周上网的时间,各自进行了抽样调查.小明调查了八年级信息技术兴趣小组中40名学生每周上网的时间,算得这些学生平均每周上网时间为2.5h;小华从全体320名八年级学生名单中随机抽取了40名学生,调查了他们每周上网的时间,算得这些学生平均每周上网时间为1.2h.小明与小华整理各自样本数据,如表所示.
时间段(h/周) | 小明抽样人数 | 小华抽样人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)
请根据上述信息,回答下列问题:
(1)你认为哪位学生抽取的样本具有代表性?_____.
估计该校全体八年级学生平均每周上网时间为_____h;
(2)在具有代表性的样本中,中位数所在的时间段是_____h/周;
(3)专家建议每周上网2h以上(含2h)的同学应适当减少上网的时间,根据具有代表性的样本估计,该校全体八年级学生中有多少名学生应适当减少上网的时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年全国中小学生“安全教育日”主题是“珍爱生命,安全伴我行”.小明骑单车上学,当他骑了一段,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校.以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
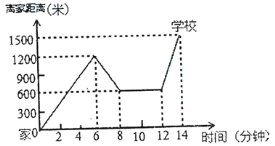
(1)小明家到学校的路程是________米;小刚在书店停留了________分钟;
(2)本次上学途中,小明全程一共用了________分钟;一共骑行了________米.
(3)我们认为骑单车的速度超过300米/分就超过了安全限度,在整个上学的途中哪个时间段小明骑车速度最快?速度在安全限度内吗?请给小明提一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
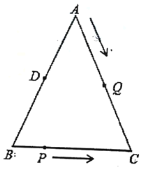
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
(1)若点P、Q两点分别从B、A两点同时出发,经过2秒后,![]() 与
与![]() 是否全等?请说明理由;
是否全等?请说明理由;
(2)若点P、Q两点分别从B、A两点同时出发,![]() 的周长为16cm,设运动时间为t,问:当t为何值时,是等腰三角形?
的周长为16cm,设运动时间为t,问:当t为何值时,是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进一批跳绳,若同时购进A种跳绳10根和B种跳绳7根,则共需395元,若同时购进A种跳绳5根和B种跳绳3根,共需185元
(1)求A、B两种跳绳的单价各是多少?
(2)若该商店准备同时购进这两种跳绳共100根,且A种跳绳的数量不少于跳绳总数量的![]() .若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
.若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
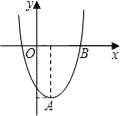
【题目】在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点![]() 从
从![]() 出发以每秒2个单位长度的速度向
出发以每秒2个单位长度的速度向![]() 运动;点
运动;点![]() 从
从![]() 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向![]() 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,连结AC交NP于Q,连结MQ.
,连结AC交NP于Q,连结MQ.
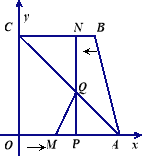
【1】点 (填M或N)能到达终点;
【1】求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
【1】是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,
![]() 说明理由.
说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com