【题目】在某市举办的“划龙舟，庆端午”比赛中，甲、乙两队在比赛时的路程
（米）与时间
（分钟）之间的函数关系图象如图所示，根据图象得到下列结论，其中错误的是（ ）
A.这次比赛的全程是500米
B.乙队先到达终点
C.比赛中两队从出发到1.1分钟时间段，乙队的速度比甲队的速度快
D.乙与甲相遇时乙的速度是375米/分钟
【答案】C
【解析】
由横纵坐标可判断A、B，观察图象比赛中两队从出发到1.1分钟时间段，乙队的图象在甲图象的下面可判断C，由图象得乙队在1.1至1.9分钟的路程为300米，可判断D．
由纵坐标看出，这次龙舟赛的全程是500m，故选项A正确；
由横坐标可以看出，乙队先到达终点，故选项B正确；
∵比赛中两队从出发到1.1分钟时间段，乙队的图象在甲图象的下面，
∴乙队的速度比甲队的速度慢，故C选项错误；
∵由图象可知，乙队在1.1分钟后开始加速，加速的总路程是500-200=300（米），加速的时间是1.9-1.1=0.8（分钟），
∴乙与甲相遇时，乙的速度是300÷0.8=375（米/分钟），故D选项正确．
故选C．
科目：初中数学 来源： 题型：
【题目】观察下列计算1+2+22+23+…+224+225的解题过程（主要步骤）。
解：设a=1+2+22+23+…+224+225，
则2a=2+22+23+…+224+225+226，
2a-a=（2+22+23+…+224+225+226）-（ 1+2+22+23+…+224+225）=226-1.
所以a=226-1.
通过阅读，你一定学到了一种解决问题的方法。请你用此方法解决下列问题：
（1）计算：1+5+52+53+…+52016+52017的值.
（2）计算：72+73+…+7n-1+7n的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图1，抛物线y=ax2+bx+3与x轴交于点B、C，与y轴交于点A，且AO=CO，BC=4．
（1）求抛物线解析式；
（2）如图2，点P是抛物线第一象限上一点，连接PB交y轴于点Q，设点P的横坐标为t，线段OQ长为d，求d与t之间的函数关系式；
（3）在（2）的条件下，过点Q作直线l⊥y轴，在l上取一点M（点M在第二象限），连接AM，使AM=PQ，连接CP并延长CP交y轴于点K，过点P作PN⊥l于点N，连接KN、CN、CM．若∠MCN+∠NKQ=45°时，求t值．
查看答案和解析>>
科目：初中数学 来源： 题型：
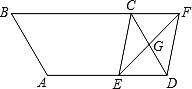
【题目】如图，在平行四边形ABCD中，AB=4cm，BC=6cm，∠B=60°，G是CD的中点，E是边AD上的动点(E不与A、D重合)，且点E由A向D运动，速度为1cm/s，EG的延长线与BC的延长线交于点F，连接CE、DF，设点E的运动时间为
(1)求证:无论
为何值,四边形CEDF都是平行四边形；
(2)①当
s时,CE⊥AD；
②当
时,平行四边形CEDF的两条邻边相等.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB.
（1）求证：PC是⊙O的切线；
（2）求证：BC=
AB；
（3）点M是弧AB的中点，CM交AB于点N，若AB=4，求MN
MC的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在△ABC中，BO、CO是角平分线．
（1）∠ABC=50°，∠ACB=60°，求∠BOC的度数，并说明理由．
（2）题（1）中，如将“∠ABC=50°，∠ACB=60°”改为“∠A=70°”，求∠BOC的度数．
（3）若∠A=n°，求∠BOC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了满足市场需求，某厂家生产A、B两种款式的环保购物袋，每天共生产5000个，两种购物袋的成本和售价如下表：
成本（元/个） | 售价 （元/个） | |
| 2 | 2.4 |
| 3 | 3.6 |
设每天生产A种购物袋x个，每天共获利y元.
（1）求y与x的函数解析式；
（2）如果该厂每天最多投入成本12000元，那么每天最多获利多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，延长BN交AC于点D，已知AB=10，BC=15，MN=3
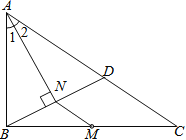
（1）求证：BN=DN；
（2）求△ABC的周长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
