【题目】观察下列计算1+2+22+23+…+224+225的解题过程（主要步骤）。
解：设a=1+2+22+23+…+224+225，
则2a=2+22+23+…+224+225+226，
2a-a=（2+22+23+…+224+225+226）-（ 1+2+22+23+…+224+225）=226-1.
所以a=226-1.
通过阅读，你一定学到了一种解决问题的方法。请你用此方法解决下列问题：
（1）计算：1+5+52+53+…+52016+52017的值.
（2）计算：72+73+…+7n-1+7n的值.
【答案】（1）
（52018﹣1）；（2）
（7n+1﹣49）
【解析】
（1）先用一个字母S表示式子的值，再在两边同时乘5，最后将两个式子相减就可以得到S的值；
（2）先用一个字母S表示式子的值，再在两边同时乘7，最后将两个式子相减就可以得到S的值.
解：（1）设S=1+5+52+53+…52016+52017，
则5S=5+52+53+…52016+52018，
5S﹣S=（5+52+53+…52016+52018）﹣（1+5+52+53+…52016+52017）=52018﹣1，
所以S=（52018﹣1）；
（2）设S=72+73+…+7n﹣1+7n，
则7S=73+…+7n+7n+1，
7S﹣S=（73+…+7n+7n+1）﹣（72+73+…+7n﹣1+7n）=7n+1﹣49，
所以S=（7n+1﹣49）.
科目：初中数学 来源： 题型：
【题目】探究题．
用棋子摆成的“T”字形图如图所示：
（1）填写表：
图形序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子个数 | 5 | 8 | … |
（2）写出第n个“T”字形图案中棋子的个数（用含n的代数式表示）；
（3）第20个“T”字形图案共有棋子多少个？
（4）计算前20个“T”字形图案中棋子的总个数．（提示：请你先思考下列问题：第1个图案与第20个图案中共有多少个棋子？第2个图案与第19个图案中共有多少个棋子？第3个图案与第18个图案呢？）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，半径为
个单位的圆片上有一点
与数轴上的原点重合，
是圆片的直径．（注：结果保留
）
把圆片沿数轴向左滚动半周，点
到达数轴上点
的位置，点表示的数是________数（填“无理”或“有理”），这个数是________
圆片在数轴上向右滚动的周数记为正数，圆片在数轴上向左滚动的周数记为负数，依次运动情况记录如下：
，
，
，
，
①第________次滚动后，点距离原点最远
②当圆片结束运动时，此时点所表示的数是________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点O为坐标原点，点A（﹣2，2）和点B（﹣3，﹣2）的位置如图所示．
（1）作出线段AB关于y轴对称的线段A′B′，并写出点A、B的对称点A′、B′的坐标；
（2）连接AA′和BB′，请在图中画一条线段，将图中的四边形AA′B′B分成两个图形，其中一个是轴对称图形，另一个是中心对称图形，并且线段的一个端点为四边形的顶点，另一个端点在四边形一边的格点上．（每个小正方形的顶点均为格点）．
查看答案和解析>>
科目：初中数学 来源： 题型：
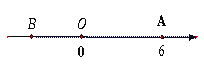
【题目】如图，已知数轴上的点A对应的数为6，B是数轴上的一点，且AB=10，动点P从点A出发，以每秒6个单位长度的速度沿着数轴向左匀速运动，设运动时间为t秒(t>0).
(1)数轴上点B对应的数是_______，点P对应的数是_______(用t的式子表示)；
(2)动点Q从点B与点P同时出发，以每秒4个单位长度的速度沿着数轴向左匀速运动，试问：运动多少时间点P可以追上点Q？
(3)M是AP的中点，N是PB的中点，点P在运动过程中，线段MN的长度是否发生变化？若有变化，说明理由；若没有变化，请你画出图形，并求出MN的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点，点M是AB边上的一个动点（不与点A重合），延长ME交CD的延长线于点N，连接MD，AN．
（1）求证：四边形AMDN是平行四边形．
（2）当AM的值为何值时，四边形AMDN是矩形？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在某市举办的“划龙舟，庆端午”比赛中，甲、乙两队在比赛时的路程
（米）与时间
（分钟）之间的函数关系图象如图所示，根据图象得到下列结论，其中错误的是（ ）
A.这次比赛的全程是500米
B.乙队先到达终点
C.比赛中两队从出发到1.1分钟时间段，乙队的速度比甲队的速度快
D.乙与甲相遇时乙的速度是375米/分钟
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
