【题目】如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点，点M是AB边上的一个动点（不与点A重合），延长ME交CD的延长线于点N，连接MD，AN．
（1）求证：四边形AMDN是平行四边形．
（2）当AM的值为何值时，四边形AMDN是矩形？请说明理由．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图，点M是直线y=2x+3上的动点，过点M作MN垂直于x轴于点N，y轴上是否存在点P，使得△MNP为等腰直角三角形，则符合条件的点P有（提示：直角三角形斜边上的中线等于斜边的一半）（ ）
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列计算1+2+22+23+…+224+225的解题过程（主要步骤）。
解：设a=1+2+22+23+…+224+225，
则2a=2+22+23+…+224+225+226，
2a-a=（2+22+23+…+224+225+226）-（ 1+2+22+23+…+224+225）=226-1.
所以a=226-1.
通过阅读，你一定学到了一种解决问题的方法。请你用此方法解决下列问题：
（1）计算：1+5+52+53+…+52016+52017的值.
（2）计算：72+73+…+7n-1+7n的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知y＝y1＋y2，y1与x成正比例，y2与x－2成正比例，当x＝1时，y＝0；当x＝－3时，y＝4.
(1)求y与x的函数关系式，并说明此函数是什么函数；
(2)当x＝3时，求y的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有理数a、b、c在数轴上的位置如图：
（1）用不等号填空：-b 0，|c| 0，|a| |b|，b-c 0，a+b 0，c-a 0.
（2）化简：
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动，它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负．例如从A到B记为：A →B（+1，+3），从B到A记为：B→A（﹣1，-3），其中第一个数表示左右方向，第二个数表示上下方向．
（1）图中A →C（______，______），B →C（______，______），C→_______（+1，﹣2）；
（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；
（3）从A处去P处的行走路线依次为（+2，+2），（+2，﹣1），（﹣2，+3），（﹣1，﹣2），请在图中标出P的位置；
（4）若图中另有两个格点M、N，且M→A（3-a，b-4），M→N（5-a，b-2），则N→A应记为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图1，抛物线y=ax2+bx+3与x轴交于点B、C，与y轴交于点A，且AO=CO，BC=4．
（1）求抛物线解析式；
（2）如图2，点P是抛物线第一象限上一点，连接PB交y轴于点Q，设点P的横坐标为t，线段OQ长为d，求d与t之间的函数关系式；
（3）在（2）的条件下，过点Q作直线l⊥y轴，在l上取一点M（点M在第二象限），连接AM，使AM=PQ，连接CP并延长CP交y轴于点K，过点P作PN⊥l于点N，连接KN、CN、CM．若∠MCN+∠NKQ=45°时，求t值．
查看答案和解析>>
科目：初中数学 来源： 题型：
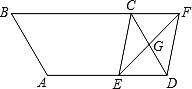
【题目】如图，在平行四边形ABCD中，AB=4cm，BC=6cm，∠B=60°，G是CD的中点，E是边AD上的动点(E不与A、D重合)，且点E由A向D运动，速度为1cm/s，EG的延长线与BC的延长线交于点F，连接CE、DF，设点E的运动时间为
(1)求证:无论
为何值,四边形CEDF都是平行四边形；
(2)①当
s时,CE⊥AD；
②当
时,平行四边形CEDF的两条邻边相等.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了满足市场需求，某厂家生产A、B两种款式的环保购物袋，每天共生产5000个，两种购物袋的成本和售价如下表：
成本（元/个） | 售价 （元/个） | |
| 2 | 2.4 |
| 3 | 3.6 |
设每天生产A种购物袋x个，每天共获利y元.
（1）求y与x的函数解析式；
（2）如果该厂每天最多投入成本12000元，那么每天最多获利多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
