
【题目】如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使得△MNP为等腰直角三角形,则符合条件的点P有(提示:直角三角形斜边上的中线等于斜边的一半)( )

A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】
根据等腰直角三角形的定义,由题意,应分两类情况讨论:当MN为直角边时和当MN为斜边时点P的位置的求法.
当M运动到(-1,1)时,ON=1,MN=1,

∵MN⊥x轴,所以由ON=MN可知,(0,0)和(0,1)就是符合条件的P点;
又当M运动到第三象限时,要MN=MP,且PM⊥MN,设点M(x,2x+3),则有-x=-(2x+3),解得x=-3,所以点P坐标为(0,-3).
如若MN为斜边时,则∠ONP=45°,所以ON=OP,设点M(x,2x+3),则有-x=-![]() (2x+3),化简得-2x=-2x-3,这方程无解,所以这时不存在符合条件的P点;
(2x+3),化简得-2x=-2x-3,这方程无解,所以这时不存在符合条件的P点;
又当点M′在第二象限,M′N′为斜边时,这时N′P=M′P,∠M′N′P=45°,设点M′(x,2x+3),则OP=ON′,而OP=![]() M′N′,∴有-x=
M′N′,∴有-x=![]() (2x+3),解得x=-
(2x+3),解得x=-![]() ,这时点P的坐标为(0,-
,这时点P的坐标为(0,-![]() ).
).
因此,符合条件的点P坐标是(0,0),(0,-![]() ),(0,-3),(0,1).
),(0,-3),(0,1).

故答案选C,


科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P , 在近岸取点Q和S , 使点P、Q、S共线且直线PS与河垂直,接着再过点S且与PS垂直的直线a上选择适当的点T , 确定PT与过点Q且垂直PS的直线b的交点R . 如果测得QS=45m , ST=90m , QR=60m , 求河的宽度PQ . 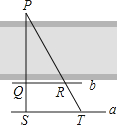
查看答案和解析>>
科目:初中数学 来源: 题型:
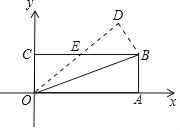
【题目】如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,E是AD延长线上一点,BE交AC于点F , 交DC于点G , 则下列结论中错误的是( ) 
A.△ABE∽△DGE
B.△CGB∽△DGE
C.△BCF∽△EAF
D.△ACD∽△GCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在五边形ABCDE中,∠B=90°,AB=BC=CD=1,AB∥CD,M是CD边的中点,点P由点A出发,按A→B→C→M的顺序运动.设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图象是( )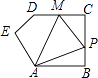
A.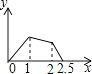
B.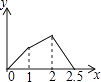
C.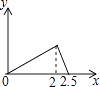
D.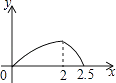
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com