
【题目】如图,□ABCD中,E是AD延长线上一点,BE交AC于点F , 交DC于点G , 则下列结论中错误的是( ) 
A.△ABE∽△DGE
B.△CGB∽△DGE
C.△BCF∽△EAF
D.△ACD∽△GCF
【答案】D
【解析】∵四边形ABCD是平行四边形 ∴AB∥CD
∴∠EDG=∠EAB
∵∠E=∠E
∴△ABE∽△DGE(第一个正确)
∵AE∥BC
∴∠EDC=∠BCG , ∠E=∠CBG
∴△CGB∽△DGE(第二个正确)
∵AE∥BC
∴∠E=∠FBC , ∠EAF=∠BCF
∴△BCF∽△EAF(第三个正确)
第四个无法证得,故选D
【考点精析】根据题目的已知条件,利用相似三角形的判定的相关知识可以得到问题的答案,需要掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线l∥AB,P为直线l上一点,且AP=AB.则点P到BC所在直线的距离是( )
A.1
B.1或 ![]()
C.1或 ![]()
D.![]() 或
或 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个钢筋三角形框架三边长分别为20厘米,50厘米、60厘米,现要再做一个与其相似的钢筋三角形框架,而只有长是30厘米和50厘米的两根钢筋,要求以其中一根为边,从另一根上截下两段(允许有余料)作为两边,则不同的截法有( ).
A.一种
B.二种
C.三种
D.四种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使得△MNP为等腰直角三角形,则符合条件的点P有(提示:直角三角形斜边上的中线等于斜边的一半)( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号):
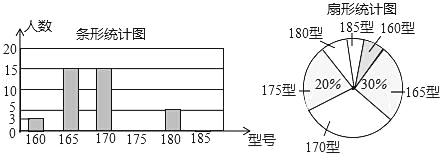
根据以上信息,解答下列问题:
(1)该班共有 名学生;
(2)补全条形统计图;
(3)该班学生所穿校服型号的众数为 ,中位数为 ;
(4)如果该校预计招收新生1500名,根据样本数据,估计新生穿170型校服的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列4组条件中,能判定△ABC∽△DEF的是( )
A.AB=5,BC=4,∠A=45°;DE=10,EF=8,∠D=45°
B.∠A=45°,∠B=55°;∠D=45°,∠F=75°
C.BC=4,AC=6,AB=9;DE=18,EF=8,DF=12
D.AB=6,BC=5,∠B=40°;DE=5,EF=4,∠E=40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2 , 则它移动的距离AA′等于( ) 

A.0.5cm
B.1cm
C.1.5cm
D.2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知A、B、C、D四点的坐标依次为(0,0)、(6,0)(8,6)、(2,6),若一次函数y=mx﹣6m的图象将四边形ABCD的面积分成1:3两部分,则m的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;
(1)小文认为菱形是特殊的“筝形”,你认为他的判断正确吗?
(2)小文根据学习几何图形的经验,通过观察、实验、归纳、类比、猜想、证明等方法,对AB≠BC的“筝形”的性质和判定方法进行了探究.下面是小文探究的过程,请补充完成:
①他首先发现了这类“筝形”有一组对角相等,并进行了证明,请你完成小文的证明过程.
已知:如图,在”筝形”ABCD中,AB=AD,CB=CD.
求证:∠ABC=∠ADC.
证明:②小文由①得到了这类“筝形”角的性质,他进一步探究发现这类“筝形”还具有其它性质,请再写出这类“筝形”的一条性质(除“筝形”的定义外);
③继性质探究后,小文探究了这类“筝形”的判定方法,写出这类“筝形”的一条判定方法(除“筝形”的定义外):
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com