
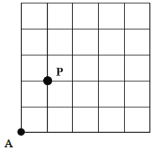
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.例如从A到B记为:A →B(+1,+3),从B到A记为:B→A(﹣1,-3),其中第一个数表示左右方向,第二个数表示上下方向.


(1)图中A →C(______,______),B →C(______,______),C→_______(+1,﹣2);
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)从A处去P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;
(4)若图中另有两个格点M、N,且M→A(3-a,b-4),M→N(5-a,b-2),则N→A应记为什么?
【答案】(1)(+3,+4),(+2,+1),D(2)10(3)图见解析(4)(-2,-2)
【解析】
(1)根据题干中“向上向右走为正,向下向左走为负,第一个数表示左右方向,第二个数表示上下方向”判断出起点到终点的移动方法和距离即可.
(2)分别计算出A到B,B到C,C到D运动的路程,再求和.
(3)按照“第一个数的正与负表示右与左移,第二个数的正与负表示上与下移动”这个规律,进行判断.可以先看左右方向表示的数字和即为左右方向移动的距离,再看上下方向表示的数字和即为上下移动的距离..
(4)把M点看作坐标原点,则A与N的坐标就分别为(3-a,b-4),(5-a,b-2),再通过坐标差值的正负来判断位置.
(1) A →C:先向右移动3个单位,再向上移动4个单位,则为(+3,+4)
B →C:先向右移动2个单位,再向上移动1个单位,则为(+2,+1)
(+1,﹣2)表示为C点向右移动1个单位,向下移动2个单位,则为C→D.
(2) A →B的路程为:1+3=4,B →C的路程为:2+1=3,C→D的路程为1+2=3
所以A→B→C→D走过的路程为4+3+3=10.
(3)左右方向的数字和为:(+2)+(+2)+(-2)+(-1)=+1,即代表向右移动了1个单位.
上下方向的数字和为:(+2)+(-1)+(+3)+(-2)=+2,即代表向上移动了2个单位.
所以,从A处去P处向右移动了2个单位,向上移动了2个单位.位置如图所示:
(4) 由M→A(3-a,b-4),M→N(5-a,b-2)可知,此时可以把M点看作坐标原点,则A点的坐标为(3-a,b-4),N点的坐标为(5-a,b-2),则N→A,左右方向,![]() ,所以A在N的左侧2个单位处.上下方向,
,所以A在N的左侧2个单位处.上下方向,![]() ,所以A在N的下方2个单位处.所以,N→A记作(-2,-2)
,所以A在N的下方2个单位处.所以,N→A记作(-2,-2)
故答案为:(1)(+3,+4),(+2,+1),D(2)10(3)图见解析(4)(-2,-2)


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,
,![]() 平分
平分![]() .
.
(1)![]() ;
;
(2)若在图1中画射线![]() ,设
,设![]() ,
,![]() 平分
平分![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的大小;
的大小;
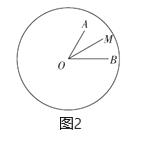
(3)如图2,若线段![]() 与
与![]() 分别为同一钟表上某一时刻的时针与分针,
分别为同一钟表上某一时刻的时针与分针,![]() ,在时针与分针转动过程中,
,在时针与分针转动过程中,![]() 始终平分
始终平分![]() ,则经过多少时间后,
,则经过多少时间后,![]() 的度数第一次等于
的度数第一次等于![]() .
.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,点A(﹣2,2)和点B(﹣3,﹣2)的位置如图所示.
(1)作出线段AB关于y轴对称的线段A′B′,并写出点A、B的对称点A′、B′的坐标;
(2)连接AA′和BB′,请在图中画一条线段,将图中的四边形AA′B′B分成两个图形,其中一个是轴对称图形,另一个是中心对称图形,并且线段的一个端点为四边形的顶点,另一个端点在四边形一边的格点上.(每个小正方形的顶点均为格点).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠DAB=60°,AB=AD,线段BC绕点B顺时针旋转60°得到线段BE,连接AC、ED.
(1)求证:AC=DE;
(2)若DC=4,BC=6,∠DCB=30°,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形.
(2)当AM的值为何值时,四边形AMDN是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于C、D两点, C点的坐标是(4,-1),D点的横坐标为-2.
的图象交于C、D两点, C点的坐标是(4,-1),D点的横坐标为-2.
(1)求反比例函数与一次函数的关系式;
(2)根据图象直接回答:当x为何值时,一次函数的值小于反比例函数的值?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 a b , a 与b 两个数在数轴上对应的点分别为点 A 、点 B ,求 A 、 B 两点之间的距离.
(探索)
小明利用绝对值的概念,结合数轴,进行探索:

(1)补全小明的探索
(应用)
(2)若点C 对应的数c ,数轴上点C 到A、B 两点的距离相等,求c .(用含a、b 的代数式表示)
(3)若点 D对应的数 d ,数轴上点 D 到 A 的距离是点 D 到 B 的距离的nn 0 倍,请探索 n 的取值范围与点 D 个数的关系,并直接写出a、b 、d、n 的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小亮、小刚、小颖一起研究一道数学题.如图,已知EF⊥AB,CD⊥AB.
小明说:“如果还知道∠CDG=∠BFE,那么能得到∠AGD=∠ACB.”
小亮说:“把小明的已知和结论倒过来,即由∠AGD=∠ACB,可得到∠CDG=∠BFE.”
小刚说:“∠AGD一定大于∠BFE.”
小颖说:“如果连结GF,那么GF一定平行于AB.”
他们四人中,有________个人的说法是正确的.( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】典典同学学完统计知识后,随机调查了她家所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图:
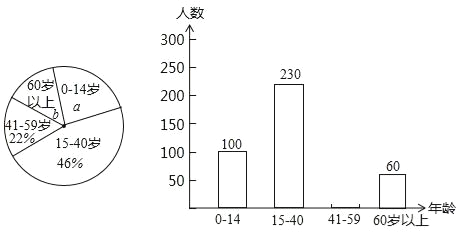
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)扇形统计图中a= ,b= ;并补全条形统计图;
(2)若该辖区共有居民3500人,请估计年龄在0~14岁的居民的人数.
(3)一天,典典知道了辖区内60岁以上的部分老人参加了市级门球比赛,比赛的老人们分成甲、乙两组,典典很想知道甲乙两组的比赛结果,王大爷告诉说,甲组与乙组的得分和为110,甲组得分不低于乙组得分的1.5倍,甲组得分最少为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com