练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于C、D两点， C点的坐标是（4，-1），D点的横坐标为-2．

    （1）求反比例函数与一次函数的关系式；

    （2）根据图象直接回答：当x为何值时，一次函数的值小于反比例函数的值？

    【答案】（1）y=-0.5x+1，y=；（2）-2<x<0或x>4.

    【解析】

    （1）先把C点坐标代入反比例函数求出m，再根据D坐标的横坐标为-2求出D点坐标，再把C,D坐标代入一次函数求出k,b的值；

    （2）根据C,D两点的横坐标，结合图像即可求解.

    （1）把C（4，-1）代入反比例函数，得m=4×（-1）=-4，

    ∴y=；

    设D（-2,y）,代入y=得y=-2，

    ∴D（-2，2）

    把C（4，-1）, D（-2，2）代入一次函数

    得

    解得k=-0.5，b=1

    ∴y=-0.5x+1

    （2）∵C,D两点的横坐标分别为4，-2，

    由图像可知当-2<x<0或x>4，一次函数的值小于反比例函数的值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，∠BAD的角平分线交BC于点E，交DC的延长线于点F，连接DE．

    （1）求证：DA＝DF；

    （2）若∠ADE＝∠CDE＝30°，DE＝2，求ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的盒子里，装有三个分别标有数字1，2，4的小球，它们的形状、大小、质地等完全相同，小明先从盒子里随机取出一个小球，记下数字为x；放回盒子摇匀后，再由小华随机取出一个小球，记下数字为y．

    （1）写出（x，y）的所有可能出现的结果；

    （2）小明、小华各取一次，由取出小球所确定的数字作为点的坐标，这样的点（x，y）中落在反比例函数y=的图象上的点的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF，连接AF，BE．

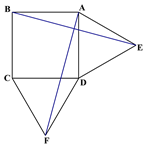
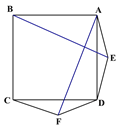
    （图1） （图2） （备用图）

    （1）请判断：AF与BE的数量关系是_____________，位置关系______________；

    （2）如图2，若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF，且EA=ED=FD=FC”，第（1）问中的结论是否仍然成立？请作出判断并给予证明；

    （3）若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论都能成立吗？请直接写出你的判断．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动，它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负．例如从A到B记为：A →B（+1，+3），从B到A记为：B→A（﹣1，-3），其中第一个数表示左右方向，第二个数表示上下方向．

    （1）图中A →C（______，______），B →C（______，______），C→_______（+1，﹣2）；

    （2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；

    （3）从A处去P处的行走路线依次为（+2，+2），（+2，﹣1），（﹣2，+3），（﹣1，﹣2），请在图中标出P的位置；

    （4）若图中另有两个格点M、N，且M→A（3-a，b-4），M→N（5-a，b-2），则N→A应记为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A、B两地果园分别有橘子40吨和60吨，C、D两地分别需要橘子30吨和70吨；已知从A、B到C、D的运价如表：

    到C地

    到D地

    A果园

    每吨15元

    每吨12元

    B果园

    每吨10元

    每吨9元

    （1）若从A果园运到C地的橘子为x吨，则从A果园运到D地的橘子为 吨，从A果园将橘子运往D地的运输费用为 元.

    （2）用含x的式子表示出总运输费（要求：列式、化简）

    （3）若这批橘子在C地和D地进行再加工，经测算，全部橘子加工完毕后总成本为w元，且.则当x= 时，w有最 值（填“大”或“小”），这个值是 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动，为了解学生对四种项目的喜欢情况，随机调查了该校m名学生最喜欢的一种项目（每名学生必选且只能选择四种活动项目的一种），并将调查结果绘制成如下的不完整的统计图表：

    学生最喜欢的活动项目的人数统计表

    项目

    学生数（名）

    百分比

    丢沙包

    20

    10%

    打篮球

    60

    p%

    跳大绳

    n

    40%

    踢毽球

    40

    20%

    根据图表中提供的信息，解答下列问题：

    （1）m= ，n= ，p= ；

    （2）请根据以上信息直接补全条形统计图；

    （3）根据抽样调查结果，请你估计该校2000名学生中有多少名学生最喜欢跳大绳．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用火柴棒按下列方式搭建三角形：

    （1）填表：

    三角形个数

    1

    2

    3

    4

    …

    火柴棒根数

    …

    （2）当三角形的个数为时，火柴棒的根数是多少？

    （3）求当时，有多少根火柴棒？

    （4）当火柴棒的根数为2017时，三角形的个数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：

    解答“已知x﹣y=2，且x＞1，y＜0，试确定x+y的取值范围”有如下解法

    解：∵x﹣y=2，∴x=y+2 又∵x＞1∴y+2＞1∴y＞﹣1

    又∵y＜0∴﹣1＜y＜0…①

    同理可得1＜x＜2…②

    由①+②得：﹣1+1＜x+y＜0+2∴x+y的取值范围是0＜x+y＜2

    按照上述方法，完成下列问题：

    （1）已知x﹣y=3，且x＞2，y＜1，则x+y的取值范围是　 　

    （2）已知关于x，y的方程组的解都是正数

    ①求a的取值范围；②若a﹣b=4，求a+b的取值范围．

    查看答案和解析>>

    同步练习册答案