
【题目】阅读下列材料:
解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法
解:∵x﹣y=2,∴x=y+2 又∵x>1∴y+2>1∴y>﹣1
又∵y<0∴﹣1<y<0…①
同理可得1<x<2…②
由①+②得:﹣1+1<x+y<0+2∴x+y的取值范围是0<x+y<2
按照上述方法,完成下列问题:
(1)已知x﹣y=3,且x>2,y<1,则x+y的取值范围是
(2)已知关于x,y的方程组![]() 的解都是正数
的解都是正数
①求a的取值范围;②若a﹣b=4,求a+b的取值范围.
【答案】(1)1<x+y<5(2)①a>1②﹣2<a+b<8
【解析】试题分析:(1)模仿阅读材料解答即可;
(2)①先把不等式组解出,再根据解为正数列关于a的不等式组解出即可;
②分别求a、b的取值,相加可得结论.
试题解析:
(1)∵x﹣y=3,
∴x=y+3,
∵x>2,
∴y+3>2,
∴y>﹣1,
又∵y<1,
∴﹣1<y<1…①
同理可得2<x<4…②
由①+②得:﹣1+2<x+y<1+4,
∴x+y的取值范围是1<x+y<5,
故答案为:1<x+y<5;
(2)①解方程组![]()
解得![]() ,
,
∵x>0,y>0,
∴![]() ,
,
解不等式组得:a>1,
∴a的取值范围为:a>1;
②)∵a﹣b=4,a>1,
∴a=b+4>1,
∴b>﹣3,
∴a+b>﹣2;
又∵a+b=2b+4,b<2,
∴a+b<8.
故﹣2<a+b<8,
a+b的取值范围为:﹣2<a+b<8.


科目:初中数学 来源: 题型:
【题目】如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(﹣1,0)、B(4,﹣1)、C(3,2).
(1)在所给的直角坐标系中画出△ABC;
(2)把△ABC向左平移3个单位,再向上平移2个单位得到△A′B′C′,画出△A′B′C′并写出点C′的坐标;
(3)求△A′B′C′的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣ ![]() ,﹣
,﹣ ![]() }=;若min{(x﹣1)2 , x2}=1,则x= .
}=;若min{(x﹣1)2 , x2}=1,则x= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨辉是我国南宋时期杰出的数学家和教育家,下图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题:
(1)图中给出了七行数字,根据构成规律,第8行中从右边数第4个数是_______;
(2)利用不完全归纳法探索出第![]() 行中的所有数字之和为_________.
行中的所有数字之和为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知图,正方形ABCD,M是BC延长线上一点,过B作BE⊥DM于点E,交DC于点F,过F作FG∥BC交BD于点G,连接GM,若S△EFD= ![]() DF2 , AB=4
DF2 , AB=4 ![]() ,则GM= .
,则GM= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.
(1)求证:BD∥EF;
(2)若 ![]() =
= ![]() ,BE=4,求EC的长.
,BE=4,求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
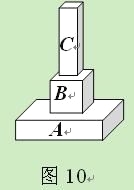
【题目】(11·大连)(本题10分)如图10,某容器由A、B、C三个长方体组成,其中
A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是容器容积的![]() (容器各面的厚
(容器各面的厚
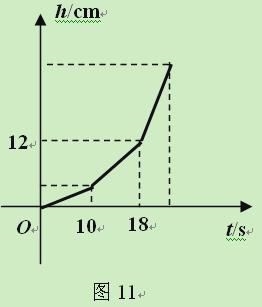
度忽略不计).现以速度v(单位:cm3/s)均匀地向容器注水,直至注满为止.图11是注水
全过程中容器的水面高度h(单位:cm)与注水时间t(单位:s)的函数图象.
⑴在注水过程中,注满A所用时间为______s,再注满B又用了_____s;
⑵求A的高度hA及注水的速度v;
⑶求注满容器所需时间及容器的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0,其中k为常数.
(1)求证:无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com