
【题目】已知图,正方形ABCD,M是BC延长线上一点,过B作BE⊥DM于点E,交DC于点F,过F作FG∥BC交BD于点G,连接GM,若S△EFD= ![]() DF2 , AB=4
DF2 , AB=4 ![]() ,则GM= .
,则GM= . 
【答案】8( ![]() ﹣1)
﹣1)
【解析】解:如图,作EH⊥CD于H,CN⊥DM于N,NK⊥CD于K.
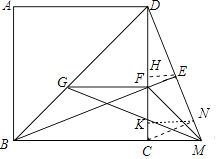
∵四边形ABCD是正方形,
∴∠BCF=∠DCM=90°,BC=DC,
∵BE⊥DM,
∴∠BEM=90°,
∴∠CBF+∠BME=90°,∠BME+∠CDM=90°,
∴∠CBF=∠CDM,
∴△BCF≌△DCM,
∴BF=DM,CF=CM,
∴∠FMB=∠GBM=45°,
∵FG∥BM,
∴四边形BMFG是等腰梯形,
∴GM=BF=DM,
∵S△DEF= ![]() DFEH=
DFEH= ![]() DF2,
DF2,
∴EH= ![]() DF,即DF=4EH,
DF,即DF=4EH,
∵△DEF∽△DNC∽△DCM,
∴CD=4NK,DM=4CN,
∵AB=CD=4 ![]() ,
,
∴NK= ![]() ,设CK=x,则DK=4
,设CK=x,则DK=4 ![]() ﹣x,
﹣x,
∵△DKN∽△NKC,
∴NK2=DKKC,
∴2=x(4 ![]() ﹣x),
﹣x),
∴x=2 ![]() ﹣
﹣ ![]() 或2
或2 ![]() +
+ ![]() (舍弃),
(舍弃),
在Rt△CKN中,CN= ![]() =
= ![]() =2(
=2( ![]() ﹣1),
﹣1),
∴GM=DM=4CN=8( ![]() ﹣1).
﹣1).
所以答案是8( ![]() ﹣1).
﹣1).
【考点精析】掌握三角形的面积和勾股定理的概念是解答本题的根本,需要知道三角形的面积=1/2×底×高;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】阅读下列材料:
解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法
解:∵x﹣y=2,∴x=y+2 又∵x>1∴y+2>1∴y>﹣1
又∵y<0∴﹣1<y<0…①
同理可得1<x<2…②
由①+②得:﹣1+1<x+y<0+2∴x+y的取值范围是0<x+y<2
按照上述方法,完成下列问题:
(1)已知x﹣y=3,且x>2,y<1,则x+y的取值范围是
(2)已知关于x,y的方程组![]() 的解都是正数
的解都是正数
①求a的取值范围;②若a﹣b=4,求a+b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点![]() 的坐标.
的坐标.
(1)点![]() 在
在![]() 轴上;
轴上;
(2)点![]() 的横坐标比纵坐标大2;
的横坐标比纵坐标大2;
(3)点![]() 在过
在过![]() ,且与
,且与![]() 轴平行的直线上.
轴平行的直线上.
(4)点![]() 在到两个坐标轴的距离相等.
在到两个坐标轴的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]() 三点.
三点.
(1)在平面直角坐标中画出![]() ,求
,求![]() 的面积
的面积
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() 使得
使得![]() 的面积等于
的面积等于![]() 的面积?若存在,求出点
的面积?若存在,求出点![]() 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
(3)如果在第二象限内有一点![]() ,用含
,用含![]() 的式子表示四边形
的式子表示四边形![]() 的面积;
的面积;
(4)且四边形![]() 的面积是
的面积是![]() 的面积的三倍,是否存在点
的面积的三倍,是否存在点![]() ,若存在,求出满足条件的
,若存在,求出满足条件的![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往.如图,a,b分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则下列判断错误的是( )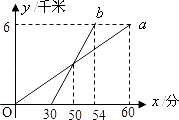
A.骑车的同学比步行的同学晚出发30分钟
B.步行的速度是6千米/小时
C.骑车的同学从出发到追上步行的同学用了20分钟
D.骑车的同学和步行的同学同时到达目的地
查看答案和解析>>
科目:初中数学 来源: 题型:
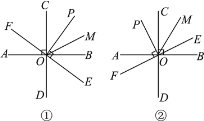
【题目】如图,已知O为直线AB上的一点,CD⊥AB于点O,PO⊥OE于点O,OM平分∠COE,点F在OE的反向延长线上.
(1)当OP在∠BOC内,OE在∠BOD内时,如图①所示,直接写出∠POM和∠COF之间的数量关系;
(2)当OP在∠AOC内且OE在∠BOC内时,如图②所示,试问(1)中∠POM和∠COF之间的数量关系是否发生变化?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com