
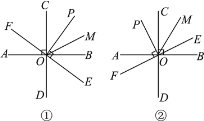
【题目】如图,已知O为直线AB上的一点,CD⊥AB于点O,PO⊥OE于点O,OM平分∠COE,点F在OE的反向延长线上.
(1)当OP在∠BOC内,OE在∠BOD内时,如图①所示,直接写出∠POM和∠COF之间的数量关系;
(2)当OP在∠AOC内且OE在∠BOC内时,如图②所示,试问(1)中∠POM和∠COF之间的数量关系是否发生变化?并说明理由.
【答案】(1)∠POM=![]() ∠COF,理由见解析;(2)∠POM=
∠COF,理由见解析;(2)∠POM=![]() ∠COF,理由见解析
∠COF,理由见解析
【解析】
(1)利用垂直的定义,CD⊥AB,PO⊥EO,等量代换得∠COP=∠BOE,利用角平分线的性质,得∠POM=![]() ∠POB=
∠POB=![]() (90°-∠POC),∠COF=90°-∠COP,得出结论;
(90°-∠POC),∠COF=90°-∠COP,得出结论;
(2)利用垂直的定义,同角的余角相等可得∠COP=∠AOF,可推出∠COP+∠COB=∠AOF+∠AOC,即∠BOP=∠COF,由对顶角相等得∠AOF=∠BOE=∠COP,利用角平分线的性质,得∠COP+∠COM=∠BOE+∠MOE,即∠POM=![]() ∠BOP,等量代换得出结论.
∠BOP,等量代换得出结论.
解:(1)∠POM=![]() ∠COF.
∠COF.
证明:∵CD⊥AB,
∴∠COP+∠BOP=90°,
∵OP⊥OE,
∴∠BOE+∠BOP=90°,
∴∠COP=∠BOE,
∵OM平分∠COE,
∴∠POM=∠MOB=![]() ∠POB=
∠POB=![]() (90°∠POC),
(90°∠POC),
∵∠COF=90°∠COP,
∴∠POM=![]() ∠COF;
∠COF;
(2)不发生变化.理由:∵CD⊥AB于点O,
∴∠AOP+∠COP=90°.
∵PO⊥OE于点O,
∴∠AOP+∠AOF=90°,
∴∠COP=∠AOF.
又∵∠AOC=∠COB=90°,
∴∠COP+∠COB=∠AOF+∠AOC,
即∠BOP=∠COF.
∵∠AOF=∠BOE,∴∠COP=∠BOE.
∵OM平分∠COE,∴∠COM=∠MOE,
∴∠COP+∠COM=∠BOE+∠MOE,
∴∠POM=![]() ∠BOP,
∠BOP,
∴∠POM=![]() ∠COF.
∠COF.
故答案为:(1)∠POM=![]() ∠COF,理由见解析;(2)∠POM=
∠COF,理由见解析;(2)∠POM=![]() ∠COF,理由见解析.
∠COF,理由见解析.


科目:初中数学 来源: 题型:
【题目】已知图,正方形ABCD,M是BC延长线上一点,过B作BE⊥DM于点E,交DC于点F,过F作FG∥BC交BD于点G,连接GM,若S△EFD= ![]() DF2 , AB=4
DF2 , AB=4 ![]() ,则GM= .
,则GM= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解八年级学生体育测试项目男女长跑的成绩,体育老师从八年级的学生中随机抽取了部分学生进行测试,并根据测试收集的数据绘制了如下两幅不完整的统计图.根据上述信息,解答下列问题:
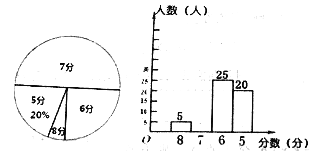
(1)本次随机抽取的学生人数为 人;
(2)将条形统计图补充完整,并求出扇形统计图中成绩为6分所对应的扇形的圆心角的度数;
(3)体育成绩在6.5分以上为合格,试估算八年级1600名学生中有多少名学生的体育成绩合格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长途汽车客运公司规定旅客可随身携带一定重量的行李,如果超过规定,则需要购买行李票,行李票费用y(元)是行李重量x(千克)的一次函数,其图象如图7所示.求出y与x之间的函数关系式,并说明行李的重量不超过多少千克,就可以免费托运?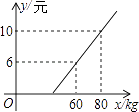
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0,其中k为常数.
(1)求证:无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
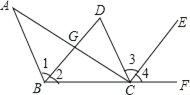
【题目】如图,AB∥CD,BD平分∠ABC,CE平分∠DCF,∠ACE=90°.
(1)判断BD和CE的位置关系,并说明理由;
(2)判断AC和BD是否垂直,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90,AC=12cm,BC=24cm,动点P从点A开始沿边AC向点C以2cm/s的速度移动.动点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果P、Q分别从点A、B同时出发,那么△PCQ的面积S随出发时间t如何变化?(写出函数关系式及t的取值范围) 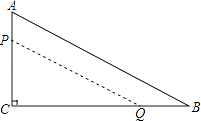
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1) 求证:AD=AF;
(2) 当△ABC满足什么条件时,四边形ADCF是矩形.并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com