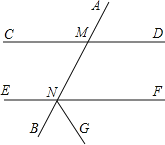
【题目】如图，已知NG平分∠BNF，∠AMD=∠MNF，∠CMN：∠DMN=3：5，试求∠MNF和∠GNF的度数．
【答案】∠MNF=67.5°，∠GNF=56.25°
【解析】
先利用平角的定义得到∠CMN=67.5°，∠CMN=112.5°，再根据平行线的判定由∠AMD=∠MNF得到CD∥EF，于是根据平行线的性质得∠MNF=∠CMN=67.5°，∠BNF=∠DMN=112.5°，然后根据角平分线的定义求∠GNF的度数．
解：∵∠CMN：∠DMN=3：5，
而∠CMN+∠DMN=180°，
∴∠CMN=
×180°=67.5°，∠CMN=
×180°=112.5°，
∵∠AMD=∠MNF，
∴CD∥EF，
∴∠MNF=∠CMN=67.5°，
∠BNF=∠DMN=112.5°，
∵NG平分∠BNF，
∴∠GNF=
∠BNF=56.25°．
科目：初中数学 来源： 题型：
【题目】尺规作图，不写作法，保留作图痕迹．
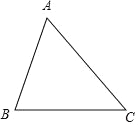
如图，△ABC中，∠A＝60°．
（1）试求作一点P，使得点P到B、C两点的距离相等，并且到AB、BC两边的距离也相等（尺规作图，不写作法，保留作图痕迹）．
（2）在（1）的条件下，若∠ACP＝15°，求∠BPC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，点P是直线l3上一动点
（1）如图1，当点P在线段CD上运动时，∠PAC，∠APB，∠PBD之间存在什么数量关系？请你猜想结论并说明理由．
（2）当点P在C、D两点的外侧运动时（P点
与点C、D不重合，如图2和图3），上述（1）中的结论是否还成立？若不成立，请直接写出∠PAC，∠APB，∠PBD之间的数量关系，不必写理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
，
，
，试说明：
．
完善下面的解答过程，并填写理由或数学式．
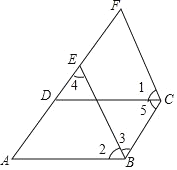
解：因为（已知）
所以
__________．
所以
（_________________）．
因为（已知）
所以
_________．
所以
，
所以
（_______________．）
即：
．
因为（已知）
所以
（___________________．）
即：
．
所以（_____________________．）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于实数p，q，我们用符号min{p，q}表示p，q两数中较小的数，如min{1，2}=1，因此，min{﹣ 
，﹣ 
}=；若min{（x﹣1）2 ， x2}=1，则x= ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线AB，CD相交于点O，OE⊥AB，OF⊥CD.
(1)若OC恰好是∠AOE的平分线，则OA是∠COF的平分线吗？请说明理由；
(2)若∠EOF＝5∠BOD，求∠COE的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知图，正方形ABCD，M是BC延长线上一点，过B作BE⊥DM于点E，交DC于点F，过F作FG∥BC交BD于点G，连接GM，若S△EFD= 
DF2 ， AB=4 
，则GM= ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了解八年级学生体育测试项目男女长跑的成绩，体育老师从八年级的学生中随机抽取了部分学生进行测试，并根据测试收集的数据绘制了如下两幅不完整的统计图.根据上述信息，解答下列问题：
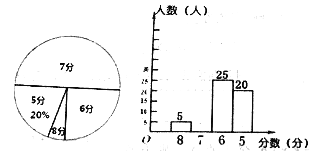
（1）本次随机抽取的学生人数为 人；
（2）将条形统计图补充完整，并求出扇形统计图中成绩为6分所对应的扇形的圆心角的度数；
（3）体育成绩在6.5分以上为合格，试估算八年级1600名学生中有多少名学生的体育成绩合格.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
