【题目】用火柴棒按下列方式搭建三角形：
（1）填表：
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | … |
（2）当三角形的个数为
时，火柴棒的根数是多少？
（3）求当
时，有多少根火柴棒？
（4）当火柴棒的根数为2017时，三角形的个数是多少？
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，小明在大楼45米高（即PH=45米，且PH⊥HC）的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处的俯角为60°，已知该山坡的
坡度i（即tan∠ABC）为1： 
.（点P、H、B、C、A在同一个平面上
点H、B、C在同一条直线上）
（1）∠PBA的度数等于________度；
（2）求A、B两点间的距离（结果精确到0.1米，参考数据： 
≈1.414， 
≈1.732）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，一次函数
的图象与反比例函数
的图象交于C、D两点， C点的坐标是（4，-1），D点的横坐标为-2．
（1）求反比例函数与一次函数的关系式；
（2）根据图象直接回答：当x为何值时，一次函数的值小于反比例函数的值？
查看答案和解析>>
科目：初中数学 来源： 题型：
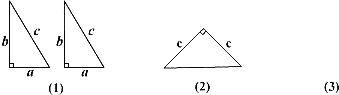
【题目】如图(1)是用硬纸板做成的两个全等的直角三角形,两直角边的长分别为
和
斜边长为
图(2)是以
为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个直角梯形.
(1)在图(3)处画出拼成的这个图形的示意图；
(2)利用(1)画出的图形证明勾股定理.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明、小亮、小刚、小颖一起研究一道数学题．如图，已知EF⊥AB，CD⊥AB.
小明说：“如果还知道∠CDG＝∠BFE，那么能得到∠AGD＝∠ACB.”
小亮说：“把小明的已知和结论倒过来，即由∠AGD＝∠ACB，可得到∠CDG＝∠BFE.”
小刚说：“∠AGD一定大于∠BFE.”
小颖说：“如果连结GF，那么GF一定平行于AB.”
他们四人中，有________个人的说法是正确的．( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
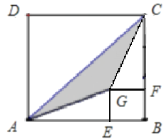
【题目】如图，正方形ABCD与正方形BFGE中，点E在边AB上，若AE=a，BE=b，（其中a＞2b）．
（1）请用含有a，b的代数式表示图中阴影部分的面积；
（2）当a=5cm，b=3cm时，求阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，∠B＜90，BC＞AB．作AE⊥BC于点E，AF⊥CD于点F，记∠EAF的度数为α，AE＝a，AF＝b．则以下选项错误的是( )
A. ∠D的度数为α
B. a∶b＝CD∶BC
C. 若α＝60，则平行四边形ABCD的周长为 
D. 若α＝60，则四边形AECF的面积为平行四边形ABCD面积的一半
查看答案和解析>>
科目：初中数学 来源： 题型：
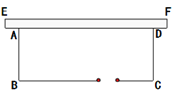
【题目】老王想靠着一面旧墙EF，开垦一块长方形的菜地ABCD，如图所示，菜地的一边靠墙，另外三边用竹篱笆围起来，并在平行于墙的一边BC上留1米宽装门，已知现有竹篱笆长共32米，全部用完.(损耗不计)
(1)设垂直于墙面的一边AB长为x米，请用含有x的代数式来表示菜园的面积.
(2)当x=8时，求菜地面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，OC是∠AOB内一条射线，OD、OE分别是∠AOC、∠BOC的平分线．
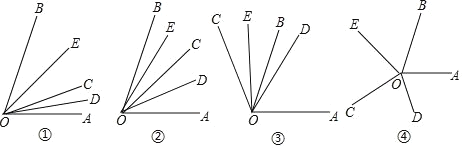
(1)如图①，当∠AOB＝80°时，∠DOE＝_______°；
(2)如图②，当射线OC在∠AOB内绕O点旋转时，∠BOE、∠EOD、∠DOA三角之间有怎样的数量关系?并说明理由；
(3)当射线OC在∠AOB外如图③所示位置时，(2）中三个角：∠BOE、∠EOD、∠DOA之间数量关系是_______；
(4)当射线OC在∠AOB外如图④所示位置时，∠BOE、∠EOD、∠DOA之间数量关系是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
