
【题目】如图,OC是∠AOB内一条射线,OD、OE分别是∠AOC、∠BOC的平分线.
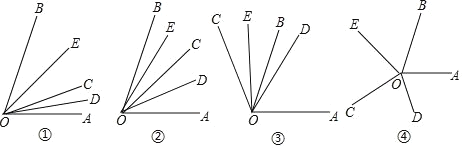
(1)如图①,当∠AOB=80°时,∠DOE=_______°;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠BOE、∠EOD、∠DOA三角之间有怎样的数量关系?并说明理由;
(3)当射线OC在∠AOB外如图③所示位置时,(2)中三个角:∠BOE、∠EOD、∠DOA之间数量关系是_______;
(4)当射线OC在∠AOB外如图④所示位置时,∠BOE、∠EOD、∠DOA之间数量关系是_______.
【答案】(1)40°(2)![]() (3)不成立,理由见解析.(4)∠DOE=∠BOE+∠DOA.
(3)不成立,理由见解析.(4)∠DOE=∠BOE+∠DOA.
【解析】
(1)(2)根据角平分线定义得出∠DOC=![]() ∠AOC,
∠AOC,![]() ,求出∠DOE=
,求出∠DOE=
![]()
![]() ,即可得出答案;
,即可得出答案;
(3)根据角平分线定义得出∠DOC=![]() ∠AOC,∠EOC=
∠AOC,∠EOC=![]() ∠BOC,求出∠DOE=
∠BOC,求出∠DOE=![]() ∠AOC-∠BOC)=
∠AOC-∠BOC)=![]() ∠AOB,即可得出答案;
∠AOB,即可得出答案;
(4)根据角平分线定义即可求解.
当射线OC在∠AOB的内部时,
∵OD,OE分别为∠AOC,∠BOC的角平分线,
∠DOC=![]() ∠AOC,∠EOC=
∠AOC,∠EOC=![]() ∠BOC,
∠BOC,
∴∠DOE=∠DOC+∠EOCP=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB,
∠AOB,
(1)若∠AOB=80°,则∠DOE的度数为40°
故答案为:40;
(2)![]()
(3)当射线OC在∠AOB的外部时(1)中的结论不成立.理由是:
∵OD、OE分别是∠AOC、∠BOC的角平分线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
(4)∵OD,OE分别为∠AOC',∠BOC的角平分线,
![]() ,
,
![]() ,
,
故∠BOE、∠EOD、∠DOA之间数量关系是:
![]()
故答案为:∠DOE=∠BOE+∠DOA.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】用火柴棒按下列方式搭建三角形:

(1)填表:
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | … |
(2)当三角形的个数为![]() 时,火柴棒的根数是多少?
时,火柴棒的根数是多少?
(3)求当![]() 时,有多少根火柴棒?
时,有多少根火柴棒?
(4)当火柴棒的根数为2017时,三角形的个数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法
解:∵x﹣y=2,∴x=y+2 又∵x>1∴y+2>1∴y>﹣1
又∵y<0∴﹣1<y<0…①
同理可得1<x<2…②
由①+②得:﹣1+1<x+y<0+2∴x+y的取值范围是0<x+y<2
按照上述方法,完成下列问题:
(1)已知x﹣y=3,且x>2,y<1,则x+y的取值范围是
(2)已知关于x,y的方程组![]() 的解都是正数
的解都是正数
①求a的取值范围;②若a﹣b=4,求a+b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
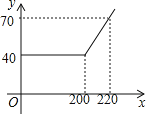
【题目】某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200小时”,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.
(1)当x≥200时,求y与x之间的函数关系式
(2)若小刚家10月份上网180小时,则他家应付多少元上网费?
(3)若小明家10月份上网费用为52元,则他家该月的上网时间是多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于任意两点A(x1,y1)B (x2,y2),规定运算:
(1)A⊕B=(x1+x2,y1+y2);
(2)A⊙B=x1x2+y1y2;
(3)当x1=x2且y1=y2时,A=B.
有下列四个命题:
①若有A(1,2),B(2,﹣1),则A⊕B=(3,1),A⊙B=0;
②若有A⊕B=B⊕C,则A=C;
③若有A⊙B=B⊙C,则A=C;
④(A⊕B)⊕C=A⊕(B⊕C)对任意点A、B、C均成立.
其中正确的命题为______(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从一副52张(没有大小王)的扑克中,每次抽出1张,然后放回洗匀再抽,在实验中得到下列表中部分数据:
实验次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
出现方块的次数 | 11 | 18 | a | 40 | 49 | 63 | 68 | 80 | 91 | 100 |
出现方块的频率 | 27.5% | 22.5% | 25% | 25% | 24.5% | 26.25% | 24.3% | b | 25% | 25% |
(1)填空a= ,b= ;
(2)从上面的图表中可以估计出现方块的概率是 ;
(3)将这幅扑克中的所有方块(即从方块1到方块13,共13张)取出,将它们背面朝上重新洗牌后,从中摸出一张,若摸出的这张牌面数字为奇数,则甲方贏,若摸出的这张牌的牌面数字是偶数,则乙方赢,你认为这个游戏对双方是公平的吗说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从超市出发,向东走了2![]() 到达小刚家,继续向东走了3
到达小刚家,继续向东走了3![]() 到达小红家,又向西走了9
到达小红家,又向西走了9![]() 到达小英家,最后回到超市.
到达小英家,最后回到超市.
(1)请以超市为原点,以向东方向为正方向,用1个单位长度表示1![]() ,画出数轴,在数轴上表示出小刚家、小红家、小英家的位置;
,画出数轴,在数轴上表示出小刚家、小红家、小英家的位置;
(2)小英家距小刚家有多远?
(3)货车一共行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,直线L:yax10a与x轴负半轴、y轴正半轴分别交于A、B两点.

(1)当OAOB时,试确定直线L的解析式;
(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AMOQ于M,BNOQ于N,若AM8,BN6,求MN的长.
(3)当a取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角OBF和等腰直角ABE,连接EF交y轴于P点,如图③,问:当点B在y轴正半轴上运动时,试猜想PB的长是否为定值,若是,请求出其值,若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com