
【题目】如图①所示,直线L:yax10a与x轴负半轴、y轴正半轴分别交于A、B两点.

(1)当OAOB时,试确定直线L的解析式;
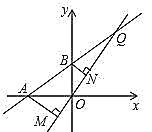
(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AMOQ于M,BNOQ于N,若AM8,BN6,求MN的长.
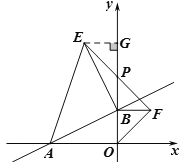
(3)当a取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角OBF和等腰直角ABE,连接EF交y轴于P点,如图③,问:当点B在y轴正半轴上运动时,试猜想PB的长是否为定值,若是,请求出其值,若不是,说明理由.
【答案】(1)L的解析式y=x+10;(2)MN =14;(3)PB的长为定值,PB=5,见解析.
【解析】
(1)先求出直线y=ax+10a与x、y轴的交点坐标,然后由OA=OB可求出a的值,进而确定直线解析式;
(2)用AAS证明△AMO≌△ONB,由全等三角形的性质得ON=AM,OM=BN,进一步即可求出MN的值;
(3)过点E作EG⊥y轴于G点,先证明△ABO≌△EGB,得BG=AO=10,OB=EG,再证明△BFP≌△GEP,得BP=GP=![]() BG=5,于是问题得解.
BG=5,于是问题得解.
解:(1)(1)∵直线L:y=ax+10a,
∴A(-10,0),B(0,10a),
∵直线交y轴正半轴,∴10a>0,∴a>0.
由OA=OB得:10a=10,∴a=1,
∴直线解析式为:y=x+10;
(2)∵AM⊥OQ,BN⊥OQ,∴∠AMO=∠BNO=90°,
∴∠AOM+∠MAO=90°,
∵∠AOM+∠BON=90°,∴∠MAO=∠NOB.
在△AMO和△OBN中,
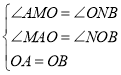
∴△AMO≌△ONB.∴ON=AM,OM=BN,
∵AM=8,BN=6,∴MN=AM+BN=14.
(3)PB的长为定值.
理由:如图,过点E作EG⊥y轴于G点,
∵△AEB为等腰直角三角形,∴AB=EB,∠ABO+∠EBG=90°,
∵EG⊥BG,∴∠GEB+∠EBG=90°.
∴∠ABO=∠GEB.
在△ABO和△EGB中
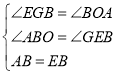
∴△ABO≌△EGB,∴BG=AO=10,OB=EG,
∵△OBF为等腰直角三角形,∴OB=BF,∴BF=EG.
在△BFP和△GEP中
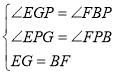
∴△BFP≌△GEP,∴BP=GP=![]() BG=5.
BG=5.
即PB的长为定值.


科目:初中数学 来源: 题型:
【题目】如图,OC是∠AOB内一条射线,OD、OE分别是∠AOC、∠BOC的平分线.
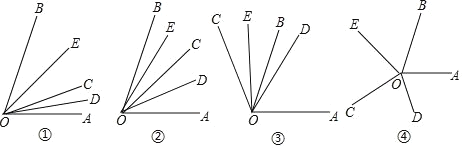
(1)如图①,当∠AOB=80°时,∠DOE=_______°;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠BOE、∠EOD、∠DOA三角之间有怎样的数量关系?并说明理由;
(3)当射线OC在∠AOB外如图③所示位置时,(2)中三个角:∠BOE、∠EOD、∠DOA之间数量关系是_______;
(4)当射线OC在∠AOB外如图④所示位置时,∠BOE、∠EOD、∠DOA之间数量关系是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.

(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
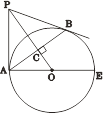
【题目】如图,已知点P是⊙O外一点,PB切⊙O于点B,BA 垂直OP于C,交⊙O于点A,连接PA、AO,延长AO,交⊙O于点E.
(1)求证:PA是⊙O的切线;
(2)若tan∠CAO=![]() ,且OC=4,求PB的长.
,且OC=4,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强环境保护意识,![]() 月
月 ![]() 日“世界环境日”当天,若干名“环境小卫士”组成了“控制噪声污染”课题学习研究小组.该小组抽样调查了全市
日“世界环境日”当天,若干名“环境小卫士”组成了“控制噪声污染”课题学习研究小组.该小组抽样调查了全市 ![]() 个噪声测量点在某时刻的噪声声级(单位:
个噪声测量点在某时刻的噪声声级(单位:![]() ),将调查的数据进行处理(设所测数据均为正整数),得频数分布表如表:
),将调查的数据进行处理(设所测数据均为正整数),得频数分布表如表:
组 别 | 噪声声级分组 | 频 数 | 频 率 |
1 | 44.5--59.5 | 4 | 0.1 |
2 | 59.5--74.5 | a | 0.2 |
3 | 74.5--89.5 | 10 | 0.25 |
4 | 89.5--104.5 | b | c |
5 | 104.5--119.5 | 6 | 0.15 |
合 计 | 40 | 1.00 |
根据表中提供的信息解答下列问题:
(1)频数分布表中的 ![]() ,
,![]() ,
,![]() ;
;
(2)补全完整频数分布直方图(如图);

(3)从这个统计中,你认为噪声污染的噪音声级分布情况怎样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了开展“阳光体育”活动,某校在大课间中开设了A:体操,B:跑操,C:舞蹈,D:健美操四项活动,为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:
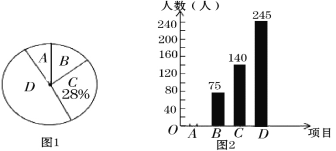
(1)本次抽查的样本容量是 ;
(2)请将统计图2补充完整;
(3)统计图1中D项目对应的扇形的圆心角是 度;
(4)已知该校共有学生3000人,请根据调查结果估计该校喜欢跑操的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示-3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m-n|.
(2)如果|x+1|=3,那么x= ;
(3)若|a-3|=2,|b+2|=1,且数a、b在数轴上表示的数分别是点A、点B,则A、B 两点间的最大距离是 .
(4)若数轴上表示a的点位于-4与2之间,则|a+4|+|a-2= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com