
【题目】小明、小亮、小刚、小颖一起研究一道数学题.如图,已知EF⊥AB,CD⊥AB.
小明说:“如果还知道∠CDG=∠BFE,那么能得到∠AGD=∠ACB.”
小亮说:“把小明的已知和结论倒过来,即由∠AGD=∠ACB,可得到∠CDG=∠BFE.”
小刚说:“∠AGD一定大于∠BFE.”
小颖说:“如果连结GF,那么GF一定平行于AB.”
他们四人中,有________个人的说法是正确的.( )

A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
根据“垂直的定义、平行线的判定与性质”结合“已知条件”进行分析判断即可.
(1)∵EF⊥AB,CD⊥AB,
∴∠BEF=∠BDC=90°,
∴CD∥EF,
∴∠BFE=∠BCD,
∵∠CDG=∠BFE,
∴∠CDG=∠BCD,
∴DG∥BC,
∴∠AGD=∠ACB,即小明的说法正确;
(2)∵∠AGD=∠ACB,
∴DG∥BC,
∴∠CDG=∠BFE,
∵EF⊥AB,CD⊥AB,
∴∠BEF=∠BDC=90°,
∴CD∥EF,
∴∠BFE=∠BCD,
∴∠CDG=∠BFE,即小亮的说法正确;
(3)∵EF⊥AB,CD⊥AB,
∴∠BEF=∠BDC=90°,
∴CD∥EF,
∴∠BFE=∠BCD,
∵∠ACB>∠BCD,
∴∠ACB>∠BFE,
但由于不知道此时DG与BC的位置关系,不能确定∠AGD与∠ACB的大小关系,
∴∠AGD一定大于∠BFE的说法不一定成立,即小刚的说法错误;
(4)如下图,连接GF,
因为由已知条件不能确定点F、G在BC和AC上的位置,
所以不能确定FG与AB的位置关系,即小颖的说法错误.
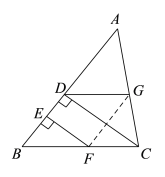
综上所述,四人的说法中,有二人的说法是正确的.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列单项式的排列规律:3x,![]() ,照这样排列第10个单项式应是
,照这样排列第10个单项式应是![]()
![]()
A. 39x10 B. -39 x10 C. -43 x10 D. 43 x10
查看答案和解析>>
科目:初中数学 来源: 题型:
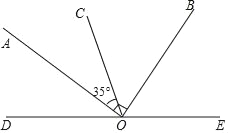
【题目】如图,O,D,E三点在同一直线上,∠AOB=90°.
(1)图中∠AOD的补角是_____,∠AOC的余角是_____;
(2)如果OB平分∠COE,∠AOC=35°,请计算出∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线![]() 射到平面镜
射到平面镜![]() 上,被
上,被![]() 反射到平面镜
反射到平面镜![]() 上,又被
上,又被![]() 反射,若被
反射,若被![]() 反射出的光线
反射出的光线![]() 与光线
与光线![]() 平行,且
平行,且![]() ,则
,则![]() _________,
_________,![]() ________.
________.
(2)在(1)中,若![]() ,则
,则![]() _______;若
_______;若![]() ,则
,则![]() ________;
________;
(3)由(1)、(2),请你猜想:当两平面镜![]() 、
、![]() 的夹角
的夹角![]() ________时,可以使任何射到平面镜
________时,可以使任何射到平面镜![]() 上的光线
上的光线![]() ,经过平面镜
,经过平面镜![]() 、
、![]() 的两次反射后,入射光线
的两次反射后,入射光线![]() 与反射光线
与反射光线![]() 平行.请说明理由.
平行.请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒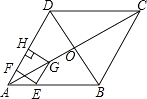
(1)求线段EF的长(用含t的代数式表示);
(2)求点H与点D重合时t的值;
(3)设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位,求S与t之间的函数关系式;
(4)矩形EFHG的对角线EH与FG相交于点O′,当OO′∥AD时,t的值为;当OO′⊥AD时,t的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明学了有理数的乘方后,知道23=8,25=32,他问老师,有没有20,2﹣3,如果有,等于多少?老师耐心提示他:25÷23=4,25﹣3=4,即25÷23=25﹣3=22=4,…“哦,我明白了了,”小明说,并且很快算出了答案,亲爱的同学,你想出来了吗?
(1)请仿照老师的方法,推算出20,2﹣3的值.
(2)据此比较(﹣3)﹣2与(﹣2)﹣3的大小.(写出计算过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com