
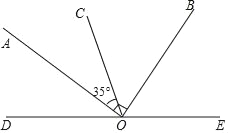
【题目】如图,O,D,E三点在同一直线上,∠AOB=90°.
(1)图中∠AOD的补角是_____,∠AOC的余角是_____;
(2)如果OB平分∠COE,∠AOC=35°,请计算出∠BOD的度数.
科目:初中数学 来源: 题型:
【题目】如图,边长12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF=3,则小正方形的边长为何?( ) 
A.![]()
B.![]()
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办一项小制作评比,作品上交时限为5月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的频数是12. 
请你回答:
(1)本次活动共有件作品参赛;
(2)若将各组所占百分比绘制成扇形统计图,那么第四组对应的扇形的圆心角是度.
(3)本次活动共评出2个一等奖和3个二等奖及三等奖、优秀奖若干名,对一、二等奖作品进行编号并制作成背面完全一致的卡片,背面朝上的放置,随机抽出两张卡片,用列表法或树状图求抽到的作品恰好一个是一等奖,一个是二等奖的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠α和∠β互补,且∠α<∠β,下列表达式:①90°﹣∠α;②∠β﹣90°;③![]() (∠β+∠α);④
(∠β+∠α);④![]() (∠β﹣∠α)中,等于∠α的余角的式子有( )
(∠β﹣∠α)中,等于∠α的余角的式子有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小亮、小刚、小颖一起研究一道数学题.如图,已知EF⊥AB,CD⊥AB.
小明说:“如果还知道∠CDG=∠BFE,那么能得到∠AGD=∠ACB.”
小亮说:“把小明的已知和结论倒过来,即由∠AGD=∠ACB,可得到∠CDG=∠BFE.”
小刚说:“∠AGD一定大于∠BFE.”
小颖说:“如果连结GF,那么GF一定平行于AB.”
他们四人中,有________个人的说法是正确的.( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形ABC中,点D在线段AB上,DE∥BC交AC于点E,点F在直线BC上,作直线EF,过点D作直线DH∥AC交直线EF于点H.
(1)在如图1所示的情况下,求证:∠HDE=∠C;
(2)若三角形ABC不变,D,E两点的位置也不变,点F在直线BC上运动.
①当点H在三角形ABC内部时,直接写出∠DHF与∠FEC的数量关系;
②当点H在三角形ABC外部时,①中结论是否依然成立?请在图2中画图探究,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com