
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.

科目:初中数学 来源: 题型:
【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
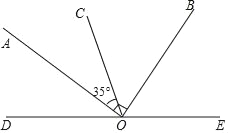
【题目】如图,O,D,E三点在同一直线上,∠AOB=90°.
(1)图中∠AOD的补角是_____,∠AOC的余角是_____;
(2)如果OB平分∠COE,∠AOC=35°,请计算出∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BAP与∠APD互补,∠1=∠2,试说明:∠E=∠F.请在下面的括号中填上理由.

解:∵∠BAP与∠APD互补( ),
∴AB∥CD( ),
∴∠BAP=∠APC( ).
又∵∠1=∠2( ),
∴∠BAP-∠1=∠APC-∠2( ),
即∠3=∠4,
∴AE∥PF( ),
∴∠E=∠F( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒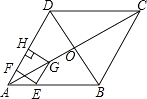
(1)求线段EF的长(用含t的代数式表示);
(2)求点H与点D重合时t的值;
(3)设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位,求S与t之间的函数关系式;
(4)矩形EFHG的对角线EH与FG相交于点O′,当OO′∥AD时,t的值为;当OO′⊥AD时,t的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O,点M,N分别为线段BO和CO的中点.求证:四边形EDNM是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
, ![]() 中,
中, ![]() 于
于![]() ,且
,且![]() .
.
(![]() )试说明
)试说明![]() 是等腰三角形.
是等腰三角形.
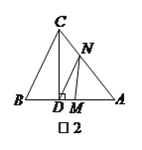
(![]() )已知
)已知![]() ,如图
,如图![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 的速度沿线段
的速度沿线段![]() 向点
向点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发以相同速度沿线段
出发以相同速度沿线段![]() 向点
向点![]() 运动,当其中一点到达终点时整个运动都停止.设点
运动,当其中一点到达终点时整个运动都停止.设点![]() 运动的时间为
运动的时间为![]() (秒).
(秒).
①若![]() 的边与
的边与![]() 平行,求
平行,求![]() 的值.
的值.
②若点![]() 是边
是边![]() 的中点,问在点
的中点,问在点![]() 运动的过程中,
运动的过程中, ![]() 能否成为等腰三角形?若能,求出
能否成为等腰三角形?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D. 
(1)若AC=4,BC=2,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com