
ΓΨΧβΡΩΓΩΧΫΨΩΧβΘ°
”ΟΤεΉ”ΑΎ≥…ΒΡΓΑTΓ±Ή÷–ΈΆΦ»γΆΦΥυ ΨΘΚ

Θ®1Θ©Χν–¥±μΘΚ
ΆΦ–Έ–ρΚ≈ | ΔΌ | ΔΎ | Δέ | Δή | Γ≠ | Δβ |
ΟΩΗωΆΦΑΗ÷–ΤεΉ”Ηω ΐ | 5 | 8 | Γ≠ |
Θ®2Θ©–¥≥ωΒΎnΗωΓΑTΓ±Ή÷–ΈΆΦΑΗ÷–ΤεΉ”ΒΡΗω ΐΘ®”ΟΚ§nΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΘΜ
Θ®3Θ©ΒΎ20ΗωΓΑTΓ±Ή÷–ΈΆΦΑΗΙ≤”–ΤεΉ”Εύ…ΌΗωΘΩ
Θ®4Θ©ΦΤΥψ«Α20ΗωΓΑTΓ±Ή÷–ΈΆΦΑΗ÷–ΤεΉ”ΒΡΉήΗω ΐΘ°Θ®Χα ΨΘΚ«κΡψœ»ΥΦΩΦœ¬Ν–Έ ΧβΘΚΒΎ1ΗωΆΦΑΗ”κΒΎ20ΗωΆΦΑΗ÷–Ι≤”–Εύ…ΌΗωΤεΉ”ΘΩΒΎ2ΗωΆΦΑΗ”κΒΎ19ΗωΆΦΑΗ÷–Ι≤”–Εύ…ΌΗωΤεΉ”ΘΩΒΎ3ΗωΆΦΑΗ”κΒΎ18ΗωΆΦΑΗΡΊΘΩΘ©
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊΫβΈωΘΜΘ®2Θ©3n+2ΗωΤεΉ”ΘΜΘ®3Θ©62ΗωΘΜΘ®4Θ©670ΗωΘ°
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ
Θ®1Θ©Ιέ≤λΓΔΖ÷ΈωΆΦ–ΈΩ…ΒΟΘΚ≥ΐ»ΞΒΎ1ΗωΆΦ–ΈΆβΘ§ΚσΟφΒΡΟΩ1ΗωΆΦ–Έ”κ«ΑΟφ1ΗωΆΦ–Έœύ±»Θ§Κα≈≈ΕύΝΥ2Ω≈ΤεΉ”Θ§ ζΝ–ΕύΝΥ1Ω≈ΤεΉ”Θ§Φ¥ΟΩ“ΜΗωΆΦ–Έ÷–ΤεΉ”ΒΡΉή ΐ±»…œ“ΜΗωΆΦ–Έ÷–ΤεΉ”ΒΡΉή ΐΕύ3Θ§”…¥ΥΩ…ΒΟΒΎnΗωΆΦΑΗ÷–Θ§ΤεΉ”ΒΡΗω ΐΈΣ5+3Θ®n©¹1Θ©Θ°’β―υΦ¥Ω…ΫβΒΟΘ®1Θ©÷ΝΘ®3Θ©–ΓΧβΒΡ¥πΑΗΘΜ
Θ®2Θ©ΫβΒΎΘ®4Θ©–ΓΧβ ±Θ§”…ΧβΡΩ÷–ΒΡΧα ΨΦΤΥψΩ…÷ΣΘ§ΒΎ1ΗωΆΦ–ΈΚΆΒΎ20ΗωΆΦ–Έ÷–Ι≤”–67Ω≈ΤεΉ”Θ§ΒΎ2ΗωΆΦ–ΈΚΆΒΎ19ΗωΆΦ–Έ÷–Ι≤”–67Ω≈Θ§Γ≠Γ≠Θ§”…¥ΥΦ¥Ω…ΒΟΘΚ«Α20ΗωΆΦ–Έ÷–ΤεΉ”Ήή ΐΈΣΘΚ67ΓΝ10=670Ω≈.
‘ΧβΫβΈωΘΚ
Ιέ≤λΓΔΖ÷ΈωΆΦ–ΈΩ…ΒΟΘΚ
ΑΎ≥…ΒΎ1ΗωΓΑTΓ±Ή÷–η“Σ5ΗωΤεΉ”ΘΜ
ΑΎ≥…ΒΎ2ΗωΓΑTΓ±Ή÷–η“Σ8ΗωΤεΉ”Θ§8©¹5=3ΘΜ
ΑΎ≥…ΒΎ3ΗωΓΑTΓ±Ή÷–η“Σ11ΗωΤεΉ”Θ§11©¹8=3ΘΜ
ΑΎ≥…ΒΎ4ΗωΓΑTΓ±Ή÷–η“Σ14ΗωΤεΉ”Θ§14©¹11=3ΘΜ
Γ≠
ΑΎ≥…ΒΎ10ΗωΓΑTΓ±Ή÷–η“Σ32ΗωΤεΉ”ΘΜ
Γ≠
”…¥ΥΩ…ΒΟ≥ωΙφ¬…ΘΚΑΎ≥…ΒΎnΗωΓΑTΓ±Ή÷–η“Σ5+3Θ®n©¹1Θ©=3n+2ΗωΤεΉ”Θ°
Θ®1Θ©ΗυΨί…œ ωΙφ¬…ΦΤΥψΧν–¥±μ÷–Υυ»± ΐΨίΈΣΘΚ
ΆΦ–Έ–ρΚ≈ | ΔΌ | ΔΎ | Δέ | Δή | Γ≠ | Δβ |
ΟΩΗωΆΦΑΗ÷–ΤεΉ”Ηω ΐ | 5 | 8 | 11 | 14 | Γ≠ | 32 |
Θ®2Θ©ΒΎnΗωΓΑTΓ±Ή÷–ΈΆΦΑΗ÷–ΤεΉ”ΒΡΗω ΐΈΣΘΚ5+3Θ®n©¹1Θ©=(3n+2)ΗωΤεΉ”ΘΜ
Θ®3Θ©ΗυΨίΒΎnΗωΓΑTΓ±Ή÷–ΈΆΦΑΗ÷–ΤεΉ”ΒΡΗω ΐΈΣ3n+2ΦΤΥψΩ…ΒΟΘΚ
ΒΎ18ΗωΓΑTΓ±Ή÷–η“Σ56ΗωΤεΉ”ΘΜΒΎ19ΗωΓΑTΓ±Ή÷–η“Σ59ΗωΤεΉ”ΘΜΒΎ20ΗωΓΑTΓ±Ή÷–η“Σ62ΗωΤεΉ”Θ§
Θ®4Θ©ΒΎ1ΗωΆΦΑΗ”κΒΎ20ΗωΆΦΑΗΙ≤”–ΘΚ5+62=67ΗωΤεΉ”ΘΜ
ΒΎ2ΗωΆΦΑΗ”κΒΎ19ΗωΆΦΑΗΙ≤”–ΘΚ8+59=67ΗωΤεΉ”ΘΜ
ΒΎ3ΗωΆΦΑΗ”κΒΎ18ΗωΆΦΑΗΙ≤”–ΘΚ11+56=67ΗωΤεΉ”ΘΜ
Γ≠Γ≠ΘΜ
”…¥ΥΩ…÷ΣΘΚ«Α20ΗωΓΑTΓΑΉ÷–ΈΆΦΑΗ÷–ΤεΉ”ΒΡΉήΗω ΐΈΣΘΚ67ΓΝ10=670Θ®ΗωΘ©Θ°


 ΜνΝΠΩΈ ±Ά§≤ΫΝΖœΑ≤αœΒΝ–¥πΑΗ
ΜνΝΠΩΈ ±Ά§≤ΫΝΖœΑ≤αœΒΝ–¥πΑΗ ―ß“Β≤βΤά“ΜΩΈ“Μ≤βœΒΝ–¥πΑΗ
―ß“Β≤βΤά“ΜΩΈ“Μ≤βœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩάΞΟς «Έ“Ο«‘ΤΡœ ΓΒΡ ΓΜαΘ§œμ”–ΓΑ¥Κ≥«Γ±÷°Οά”ΰΘ°≥ΘΉΓ»ΥΩΎ‘Φ”–668Άρ»ΥΘ§«κΫΪ668Άρ”ΟΩΤ―ßΦ« ΐΖ®±μ ΨΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ –÷Τ“©≥ß–η“ΣΫτΦ±…ζ≤ζ“Μ≈ζ“©ΤΖΘ§“Σ«σ±Ί–κ‘Ύ12ΧλΘ®Κ§12ΧλΘ©ΡΎΆξ≥…Θ°ΈΣΝΥΦ”Ωλ…ζ≤ζΘ§≥ΒΦδ≤…»ΓΙΛ»ΥΦ”ΑύΘ§ΜζΤς≤ΜΆΘΒΡ…ζ≤ζΖΫ ΫΘ§’β―υΟΩΧλ“©ΤΖΒΡ≤ζΝΩyΘ®Ε÷Θ© « ±ΦδxΘ®ΧλΘ©“Μ¥ΈΚ· ΐΘ§«“¬ζΉψ±μ÷–ΥυΕ‘”ΠΒΡ ΐΝΩΙΊœΒΘ°”…”ΎΜζΤςΗΚΚ…‘ΥΉΣ≤ζ…ζΥπΚΡΘ§ΤΫΨυ…ζ≤ζΟΩΕ÷“©ΤΖΒΡ≥…±ΨPΘ®‘ΣΘ©”κ ±ΦδxΘ®ΧλΘ©ΒΡΙΊœΒ¬ζΉψΆΦ÷–ΒΡΚ· ΐΆΦœσΘ° 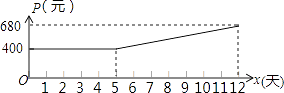
±ΦδxΘ®ΧλΘ© | 2 | 4 |
ΟΩΧλ≤ζΝΩyΘ®Ε÷Θ© | 24 | 28 |
Θ®1Θ©«σ“©ΤΖΟΩΧλΒΡ≤ζΝΩyΘ®Ε÷Θ© « ±ΦδxΘ®ΧλΘ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©Β±5ΓήxΓή12 ±Θ§÷±Ϋ”–¥≥ωPΘ®‘ΣΘ©”κ ±ΦδxΘ®ΧλΘ©ΒΡΚ· ΐΙΊœΒ «P=ΘΜ
Θ®3Θ©»τ’β≈ζ“©ΤΖΒΡΦέΗώΈΣ1400‘Σ/Ε÷Θ§ΟΩΧλΒΡάϊ»σ…ηΈΣW‘ΣΘ§«σΡΡ“ΜΧλΒΡάϊ»σΉνΗΏΘ§ΉνΗΏάϊ»σ «Εύ…ΌΘΩΘ®άϊ»σ=ΦέΗώ©¹≥…±ΨΘ©
Θ®4Θ©ΈΣΝΥΧαΗΏΙΛ»ΥΦ”ΑύΒΡΫρΧυΘ§“©≥ßΨωΕ®‘ΎΘ®3Θ©÷–ΦέΗώΒΡΜυ¥Γ…œΟΩΕ÷“©ΤΖΦ”Φέa‘ΣΘ§ΒΪ±Ί–κ¬ζΉψ¥”ΒΎ5ΧλΒΫΒΎ12ΧλΤΎΦδΘ§ΟΩΕ÷Φ”ΦέaΚσΟΩΧλΒΡάϊ»σΥφ ±ΦδΒΡ‘ω¥σΕχ‘ω¥σΘ§÷±œΏ–¥≥ωaΒΡΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΒψC‘ΎœΏΕΈAB…œΘ§«“AC©UBC=5©U2Θ§ΒψD «œΏΕΈBCΒΡ÷–ΒψΘ§ΒψE «œΏΕΈADΒΡ÷–ΒψΘ§AB=14Θ§«σœΏΕΈCEΒΡ≥Λ.
![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ4ΓΝ4’ΐΖΫ–ΈΆχΗώ÷–Θ§»Έ―Γ“ΜΗωΑΉ…ΪΒΡ–Γ’ΐΖΫ–Έ≤ΔΆΩΚΎΘ§ ΙΆΦ÷–ΚΎ…Ϊ≤ΩΖ÷ΒΡΆΦ–Έ»‘»ΜΙΙ≥…“ΜΗω÷αΕ‘≥ΤΆΦ–ΈΒΡΗ≈¬ «Θ® Θ© 
A.![]()
B.![]()
C.![]()
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ÷–Ιζ»ΥΚή‘γΩΣ Φ Ι”ΟΗΚ ΐΘ§÷–ΙζΙ≈¥ζ ΐ―ß÷χΉςΓΕΨ≈’¬Υψ θΓΖΒΡΓΑΖΫ≥ΧΓ±“Μ’¬Θ§‘Ύ άΫγ ΐ―ß Ζ…œ Ή¥Έ’ΐ Ϋ“ΐ»κΗΚ ΐΘ§»γΙϊ ’»κ1000‘ΣΦ«Ής+1000‘ΣΘ§Ρ«Ο¥©¹800‘Σ±μ Ψ( )
A. ÷ß≥ω200‘Σ B. ’»κ200‘Σ
C. ÷ß≥ω800‘Σ D. ’»κ800‘Σ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ“Ο«÷ΣΒάΘ§»Έ“β“ΜΗω’ΐ’ϊ ΐ![]() ΕΦΩ…“‘Ϋχ––’β―υΒΡΖ÷ΫβΘΚ
ΕΦΩ…“‘Ϋχ––’β―υΒΡΖ÷ΫβΘΚ ![]() Θ®
Θ®![]() Θ§
Θ§ ![]() «’ΐ’ϊ ΐΘ§«“
«’ΐ’ϊ ΐΘ§«“![]() Θ©Θ§‘Ύ
Θ©Θ§‘Ύ![]() ΒΡΥυ”–’β÷÷Ζ÷Ϋβ÷–Θ§»γΙϊ
ΒΡΥυ”–’β÷÷Ζ÷Ϋβ÷–Θ§»γΙϊ![]() Θ§
Θ§ ![]() ΝΫ“ρ ΐ÷°≤νΒΡΨχΕ‘÷ΒΉν–ΓΘ§Έ“Ο«ΨΆ≥Τ
ΝΫ“ρ ΐ÷°≤νΒΡΨχΕ‘÷ΒΉν–ΓΘ§Έ“Ο«ΨΆ≥Τ![]() «
«![]() ΒΡΉνΦ―Ζ÷ΫβΘ§≤ΔΙφΕ®ΘΚ
ΒΡΉνΦ―Ζ÷ΫβΘ§≤ΔΙφΕ®ΘΚ ![]() Θ°
Θ°
άΐ»γ![]() Ω…“‘Ζ÷Ϋβ≥…
Ω…“‘Ζ÷Ϋβ≥…![]() Θ§
Θ§ ![]() Μρ
Μρ![]() Θ§“ρΈΣ
Θ§“ρΈΣ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() «
«![]() ΒΡΉνΦ―Ζ÷ΫβΘ§Υυ“‘
ΒΡΉνΦ―Ζ÷ΫβΘ§Υυ“‘![]() Θ°
Θ°
Θ®![]() Θ©«σ≥ω
Θ©«σ≥ω![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
Θ®![]() Θ©»γΙϊ“ΜΗωΝΫΈΜ’ΐ’ϊ ΐ
Θ©»γΙϊ“ΜΗωΝΫΈΜ’ΐ’ϊ ΐ![]() Θ§
Θ§ ![]() Θ®
Θ®![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() ΈΣΉ‘»Μ ΐΘ©Θ§ΫΜΜΜΤδΗωΈΜ…œΒΡ ΐ”κ °ΈΜ…œΒΡ ΐΒΟΒΫΒΡ–¬ ΐΦθ»Ξ‘≠ά¥ΒΡΝΫΈΜ’ΐ’ϊ ΐΥυΒΟΒΡ≤νΈΣ
ΈΣΉ‘»Μ ΐΘ©Θ§ΫΜΜΜΤδΗωΈΜ…œΒΡ ΐ”κ °ΈΜ…œΒΡ ΐΒΟΒΫΒΡ–¬ ΐΦθ»Ξ‘≠ά¥ΒΡΝΫΈΜ’ΐ’ϊ ΐΥυΒΟΒΡ≤νΈΣ![]() Θ§Ρ«Ο¥Έ“Ο«≥Τ’βΗω ΐ
Θ§Ρ«Ο¥Έ“Ο«≥Τ’βΗω ΐ![]() ΈΣΓΑΈΡάΫ ΐΓ±Θ§«σΥυ”–ΓΑΈΡάΫ ΐΓ±≤Δ–¥≥ωΥυ”–ΓΑΈΡάΫ ΐΓ±÷–
ΈΣΓΑΈΡάΫ ΐΓ±Θ§«σΥυ”–ΓΑΈΡάΫ ΐΓ±≤Δ–¥≥ωΥυ”–ΓΑΈΡάΫ ΐΓ±÷–![]() ΒΡΉν–Γ÷ΒΘ°
ΒΡΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΓςABC÷–Θ§ΓœACB=90ΓψΘ§AC=BCΘ§AB=10Θ§”Ο≥ΏΙφΉςΆΦΒΡΖΫΖ®ΉςœΏΕΈADΚΆœΏΕΈDEΘ§±ΘΝτΉςΆΦΚέΦΘ»γΆΦΥυ ΨΘ§»œ’φΙέ≤λΉςΆΦΚέΦΘΘ§‘ρΓςBDEΒΡ÷ή≥Λ «Θ® Θ© 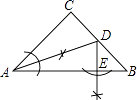
A.8
B.5 ![]()
C.![]()
![]()
D.10
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com