
【题目】在△ABC中,∠ACB=90°,AC=BC,AB=10,用尺规作图的方法作线段AD和线段DE,保留作图痕迹如图所示,认真观察作图痕迹,则△BDE的周长是( ) 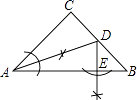
A.8
B.5 ![]()
C.![]()
![]()
D.10
科目:初中数学 来源: 题型:
【题目】探究题.
用棋子摆成的“T”字形图如图所示:

(1)填写表:
图形序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子个数 | 5 | 8 | … |
(2)写出第n个“T”字形图案中棋子的个数(用含n的代数式表示);
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.(提示:请你先思考下列问题:第1个图案与第20个图案中共有多少个棋子?第2个图案与第19个图案中共有多少个棋子?第3个图案与第18个图案呢?)
查看答案和解析>>
科目:初中数学 来源: 题型:
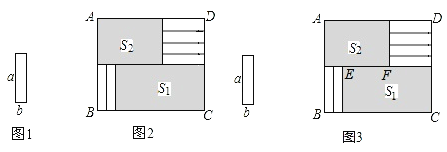
【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,求a,b满足的关系式.
(1)为解决上述问题,如图3,小明设EF=x,则可以表示出S1=_________,S2=_________;
(2)求a,b满足的关系式,写出推导过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,斜面AC的坡度为1:2,AC=3 ![]() 米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为( )
米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为( ) 
A.5米
B.6米
C.8米
D.(3+ ![]() )米
)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC,BD交于点O,下列条件中,能判定四边形ABCD为正方形的是( )
A.OA=OB=OC=OD,AB=CDB.OA=OC,OB=OD,AC⊥BD
C.OA=OB=OC=OD,AC⊥BDD.OA=OC,OB=OD,AB=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c的顶点为Q,抛物线与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.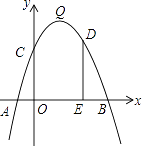
(1)求抛物线的解析式及其顶点Q的坐标;
(2)在该抛物线上求一点P,使得S△PAB=S△ABC , 求出点P的坐标:
(3)若点D是第一象限抛物线上的一个动点,过点D作DE⊥x轴,垂足为E.有一个同学说:“在第一象限抛物线上的所有点中,抛物线的顶点Q与x轴相距最远,所以当点D运动至点Q时,折线D﹣E﹣O的长度最长.”这个同学的说法正确吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com