
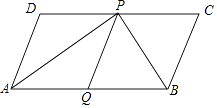
【题目】如图,在ABCD中,AP和BP分别平分∠DAB和∠CBA,PQ∥AD,若AD=5cm,AP=8cm,则△ABP的面积等于cm2 . 
【答案】24
【解析】解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA= ![]() (∠DAB+∠CBA)=90°,
(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°﹣(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在Rt△APB中,AB=10,AP=8,
∴BP= ![]() =6,
=6,
∴△ABP的面积为: ![]() ×6×8=24(cm2).
×6×8=24(cm2).
所以答案是:24.
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】2016年,某市发生了严重干旱,该市政府号召居民节约用水,为了解居民用水情况,在某小区随机抽查了10户家庭的月用水量,结果统计如图,则关于这10户家庭的月用水量,下列说法错误的是( )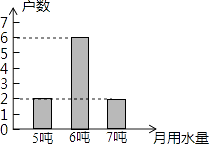
A.众数是6
B.中位数是6
C.平均数是6
D.方差是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则得到的抛物线解析式是( )
A.y=(x﹣2)2﹣3
B.y=(x﹣2)2+3
C.y=(x+2)2﹣3
D.y=(x+2)2+3
查看答案和解析>>
科目:初中数学 来源: 题型:
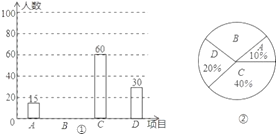
【题目】为推广阳光体育“大课间”活动,某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两幅统计图中的B补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB=4,BC=5,∠ABC=60°,对角线AC,BD交于点O,过点O作OE⊥AD,则OE等于( ) 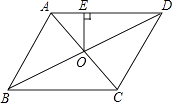
A.![]()
B.2 ![]()
C.2
D.2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线AED和矩形ABCD(不含AD)构成.矩形的长BC为8 m,宽AB为2 m.以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6 m.
(1)求抛物线的函数表达式.
(2)如果该隧道内仅设双行道,现有一辆卡车高4.2 m,宽2.4 m,那么这辆卡车能否通过该隧道?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③关于x的方程kx﹣x=a﹣b的解是x=3;④当x<3时,y1<y2中.则正确的序号有 . 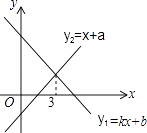
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com