
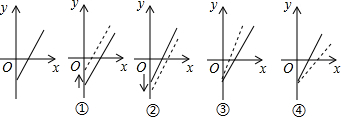
| A�� | �ڣ��� | B�� | �٣��� | C�� | �٣��� | D�� | �ܣ��� |
���� ��������4��ͼ��ı仯��֪�����ۼ۲��䣬�ܳɱ����٣����ۼ۲��䣬�ܳɱ����ӣ����ܳɱ����䣬�ۼ����ӣ����ܳɱ����䣬�ۼۼ��٣������ƶ��������������ɵó����ۣ�
��� �⣺�ٸ��ݺ���ͼ���֪��б�ʲ��䣬��y�ύ�����ƣ�
���ۼ۲��䣬�ܳɱ����٣�
�ڸ��ݺ���ͼ���֪��б�ʲ��䣬��y�ύ�����ƣ�
���ۼ۲��䣬�ܳɱ����ӣ�
�۸��ݺ���ͼ���֪��б�ʱ����y�ύ�㲻�䣬
���ܳɱ����䣬�ۼ����ӣ�
�ܸ��ݺ���ͼ���֪��б�ʱ�С����y�ύ�㲻�䣬
���ܳɱ����䣬�ۼۼ��٣�
��ʾ������1����ͼ��Ϊ�٣���ʾ������2����ͼ��Ϊ�ۣ�
��ѡB��
���� ���⿼����һ�κ�����Ӧ�ã�����Ĺؼ��Ǹ��ݺ��������ʷ���4��ͼ�������ڻ����⣬�ѶȲ������������Ŀʱ������һ�κ��������ʷ���ͼ���ǹؼ���


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
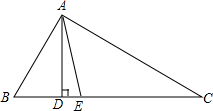 ��ͼ���ڡ�ABC�У���B=60�㣬��C=30�㣬AD��AE�ֱ��ǡ�ABC�ĸߺͽ�ƽ���ߣ����DAE�Ķ�����
��ͼ���ڡ�ABC�У���B=60�㣬��C=30�㣬AD��AE�ֱ��ǡ�ABC�ĸߺͽ�ƽ���ߣ����DAE�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=4 | B�� | x1=0��x2=4 | C�� | x=+4 | D�� | x1=2��x2=4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ֱ��l���ҵ�һ��Pʹ����A��B����ľ�����ȣ��߹���ͼ��������ͼ�ۼ���
��ֱ��l���ҵ�һ��Pʹ����A��B����ľ�����ȣ��߹���ͼ��������ͼ�ۼ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�BE�����Ľ�ƽ���ߣ���C=90�㣬D��AB���ϣ���DBΪֱ���İ�ԲO������E����BC�ڵ�F��
��ͼ����ABC�У�BE�����Ľ�ƽ���ߣ���C=90�㣬D��AB���ϣ���DBΪֱ���İ�ԲO������E����BC�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������y=-$\frac{1}{8}{x^2}+\frac{1}{2}$x+4��y�ύ�ڵ�A����x��ֱ���B��C���㣮
��ͼ��������y=-$\frac{1}{8}{x^2}+\frac{1}{2}$x+4��y�ύ�ڵ�A����x��ֱ���B��C���㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com