
分析 (1)方程两边都乘以最简公分母(x-1)化为整式方程,解整式方程可得x的值,最后检验;
(2)用加减消元法将两方程相减消去y,求得x的值,将x的值代回原方程求得y的值,可得方程组的解.
解答 解:(1)去分母,得:2-(x+2)=x-1,
去括号,得:2-x-2=x-1,
移项,得:-x-x=-1,
合并同类项,得:-2x=-1,
系数化为1,得:x=$\frac{1}{2}$,
经检验:x=$\frac{1}{2}$是原分式方程的解;
(2)解方程$\left\{\begin{array}{l}{3x+2y=15}&{①}\\{7x+2y=27}&{②}\end{array}\right.$,
②-①,得:4x=12,解得:x=3,
将x=3代入①,得:9+2y=15,
解得:y=3,
故方程组的解为:$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$.
点评 本题主要考查解分式方程和方程组的能力,将分式方程去分母转化为整式方程是解方程的关键,不要忘记检验,解方程组的思想是消元,使用何种方法需看方程中未知数系数.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=3,BC=4,P是AD上的一个动点,且与A、D不重合,过C作CQ⊥PB,垂足为Q,设BP为x,CQ为y,请写出y关于x的函数关系式y=$\frac{12}{x}$($\frac{12}{5}<x<4$).
如图,在矩形ABCD中,AB=3,BC=4,P是AD上的一个动点,且与A、D不重合,过C作CQ⊥PB,垂足为Q,设BP为x,CQ为y,请写出y关于x的函数关系式y=$\frac{12}{x}$($\frac{12}{5}<x<4$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
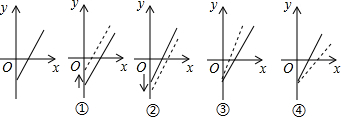
| A. | ②,③ | B. | ①,③ | C. | ①,④ | D. | ④,② |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
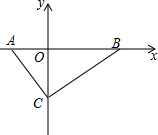 如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,顶点C在y轴的负半轴上,tan∠ABC=$\frac{3}{4}$,点P在线段OC上,且PO、PC的长(P0<PC)是x2-12x+27=0的两根.
如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,顶点C在y轴的负半轴上,tan∠ABC=$\frac{3}{4}$,点P在线段OC上,且PO、PC的长(P0<PC)是x2-12x+27=0的两根.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
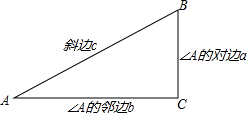 如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,我们把∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即cosA=$\frac{b}{c}$.当c=2,a=1时,求cosA.
如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,我们把∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即cosA=$\frac{b}{c}$.当c=2,a=1时,求cosA.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在四边形ABCD中,点M、N、P分别是AD、BC、BD的中点,如果$\overrightarrow{BA}=\vec a,\overrightarrow{DC}=\vec b$,那么$\overrightarrow{MN}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$.(用$\vec a和\vec b$表示)
如图,在四边形ABCD中,点M、N、P分别是AD、BC、BD的中点,如果$\overrightarrow{BA}=\vec a,\overrightarrow{DC}=\vec b$,那么$\overrightarrow{MN}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$.(用$\vec a和\vec b$表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com