
 ČēĶ¼£¬ŌŚĖıߊĪABCDÖŠ£¬µćM”¢N”¢P·Ö±šŹĒAD”¢BC”¢BDµÄÖŠµć£¬Čē¹ū$\overrightarrow{BA}=\vec a£¬\overrightarrow{DC}=\vec b$£¬ÄĒĆ“$\overrightarrow{MN}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$£®£ØÓĆ$\vec aŗĶ\vec b$±ķŹ¾£©
ČēĶ¼£¬ŌŚĖıߊĪABCDÖŠ£¬µćM”¢N”¢P·Ö±šŹĒAD”¢BC”¢BDµÄÖŠµć£¬Čē¹ū$\overrightarrow{BA}=\vec a£¬\overrightarrow{DC}=\vec b$£¬ÄĒĆ“$\overrightarrow{MN}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$£®£ØÓĆ$\vec aŗĶ\vec b$±ķŹ¾£© ·ÖĪö øł¾ŻČż½ĒŠĪµÄÖŠĪ»ĻßĘ½ŠŠÓŚµŚČż±ß²¢ĒŅµČÓŚµŚČż±ßµÄŅ»°ė±ķŹ¾³ö$\overrightarrow{PM}$”¢$\overrightarrow{PN}$£¬Č»ŗóŌŁĄūÓĆČż½ĒŠĪ·ØŌņĒó½ā¼“æÉ£®
½ā“š ½ā£ŗ”ßµćM”¢N”¢P·Ö±šŹĒAD”¢BC”¢BDµÄÖŠµć£¬
”ą$\overrightarrow{PM}$=$\frac{1}{2}$$\overrightarrow{BA}$=$\frac{1}{2}$$\overrightarrow{a}$£¬$\overrightarrow{PN}$=$\frac{1}{2}$$\overrightarrow{PN}$=$\frac{1}{2}$$\overrightarrow{b}$£¬
”ą$\overrightarrow{MN}$=$\overrightarrow{PN}$-$\overrightarrow{PM}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$£®
¹Ź“š°øĪŖ£ŗ$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$£®
µćĘĄ ±¾Ģāæ¼²éĮĖĘ½ĆęĻņĮæ£¬Čż½ĒŠĪµÄÖŠĪ»ĻßĘ½ŠŠÓŚµŚČż±ß²¢ĒŅµČÓŚµŚČż±ßµÄŅ»°ė£¬ŹģĮ·ÕĘĪÕĻņĮæµÄČż½ĒŠĪ·ØŌņŹĒ½āĢāµÄ¹Ų¼ü£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬OŹĒÖ±ĻßABÉĻµÄŅ»µć£¬ÉäĻßOC£¬OE·Ö±šĘ½·Ö”ĻAODŗĶ”ĻBOD£®
ČēĶ¼£¬OŹĒÖ±ĻßABÉĻµÄŅ»µć£¬ÉäĻßOC£¬OE·Ö±šĘ½·Ö”ĻAODŗĶ”ĻBOD£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬Å×ĪļĻßy=-$\frac{1}{8}{x^2}+\frac{1}{2}$x+4ÓėyÖį½»ÓŚµćA”¢ÓėxÖį·Ö±š½»ÓŚB”¢CĮ½µć£®
ČēĶ¼£¬Å×ĪļĻßy=-$\frac{1}{8}{x^2}+\frac{1}{2}$x+4ÓėyÖį½»ÓŚµćA”¢ÓėxÖį·Ö±š½»ÓŚB”¢CĮ½µć£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ŅŃÖŖ£ŗČēĶ¼£¬ŌŚÖ±½ĒĢŻŠĪÖ½Ę¬ABCDÖŠ£¬DC”ĪAB£¬AB£¾CD£¾AD£¬”ĻA=90”ć£¬½«Ö½Ę¬ŃŲ¹żµćDµÄÖ±Ļß·ÕŪ£¬Ź¹µćAĀäŌŚ±ßCDÉĻµÄµćE“¦£¬ÕŪŗŪĪŖDF£¬ĮŖ½įEF²¢Õ¹æŖÖ½Ę¬£®
ŅŃÖŖ£ŗČēĶ¼£¬ŌŚÖ±½ĒĢŻŠĪÖ½Ę¬ABCDÖŠ£¬DC”ĪAB£¬AB£¾CD£¾AD£¬”ĻA=90”ć£¬½«Ö½Ę¬ŃŲ¹żµćDµÄÖ±Ļß·ÕŪ£¬Ź¹µćAĀäŌŚ±ßCDÉĻµÄµćE“¦£¬ÕŪŗŪĪŖDF£¬ĮŖ½įEF²¢Õ¹æŖÖ½Ę¬£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ¼ĘĖćĻĀĮŠø÷Ģā£ŗ
¼ĘĖćĻĀĮŠø÷Ģā£ŗ²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | $\frac{1}{9}$ | B£® | $\frac{1}{6}$ | C£® | $\frac{1}{3}$ | D£® | $\frac{1}{2}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
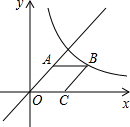 ČēĶ¼£¬OABCĪŖĮāŠĪ£¬µćCŌŚxÖįÉĻ£¬µćAŌŚÖ±Ļßy=xÉĻ£¬µćBŌŚy=$\frac{k}{x}$£Øk£¾0£©µÄĶ¼ĻóÉĻ£¬ČōSĮāŠĪOABC=$\sqrt{2}$£¬ŌņkµÄÖµĪŖ$\sqrt{2}$+1£®
ČēĶ¼£¬OABCĪŖĮāŠĪ£¬µćCŌŚxÖįÉĻ£¬µćAŌŚÖ±Ļßy=xÉĻ£¬µćBŌŚy=$\frac{k}{x}$£Øk£¾0£©µÄĶ¼ĻóÉĻ£¬ČōSĮāŠĪOABC=$\sqrt{2}$£¬ŌņkµÄÖµĪŖ$\sqrt{2}$+1£®²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com