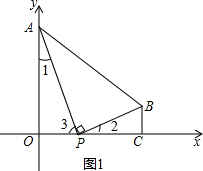
解:(1)如图1所示:
∵PA⊥PB,
∴∠2+∠3=90°,
∵AO⊥x轴,
∴∠1=∠2,
又∵BC⊥x轴,AO⊥x轴,
∴∠BCP=∠POA=90°,
∴△BCP∽△POA,
∴
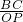
=
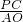
,
∵点A(0,4)、B(4,1),
∴AO=4,BC=1,OC=4,
∴
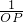
=
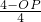
,
解得:OP=2,
∴P(2,0);
(2)设过点A,B,P三点的抛物线的解析式为:y=ax
2+bx+c,
∵点A(0,4)、B(4,1),
∴
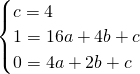
,
解得:
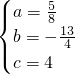
,
故抛物线解析式为:y=

x
2-

x+4;
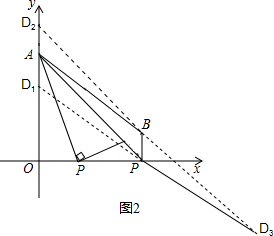
(3)如图2所示:当AB=PD
1,AB∥PD
1,此时AD
1PB是平行四边形,AD
1=PB=1,AO=4,则OD
1=3,
故D
1(0,3),利用抛物线过点A,则抛物线向下平移1个单位即可过点D
1;
当AP=BD
2,AP∥BD
2,此时AD
2BP是平行四边形,AD
2=PB=1,AO=4,则OD
2=5,
故D
2(0,5),利用抛物线过点A,则抛物线向上平移1个单位即可过点D
2;
当AB=PD
3,AB∥PD
3,此时APD
3B是平行四边形,PD
3=AB=5,A点和D
3点到PB距离相等为4,则点D
3到x轴距离为3,
故D
3(8,-3),∵y=

x
2-

x+4=

(x-
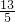
)
2-
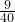
,
∴设抛物线向下平移h个单位,则过点(8,-3),故-3=

(8-
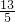
)
2-
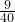
-h,
解得:h=21,
故抛物线向下平移21个单位即可过点D
3.
分析:(1)利用垂直的性质首先得出∠1=∠2,进而得出△BCP∽△POA,根据
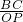
=
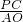
,求出OP的长即可得出P点坐标;
(2)利用点A,B,P三点的坐标,利用待定系数法求二次函数解析式y=ax
2+bx+c,即可得出答案;
(3)利用平行四边形的性质分别利用当AB=PD
1,AB∥PD
1,当AP=BD
2,AP∥BD
2,当AB=PD
3,AB∥PD
3,求出D点坐标,进而得出平移距离.
点评:此题主要考查了二次函数综合应用以及相似三角形的判定与性质、待定系数法求二次函数解析式以及平行四边形的性质和图象的平移等知识,利用数形结合得出P点坐标以及D点位置是解题关键.

 如图,已知点A(0,4)、B(4,1),BC⊥x轴于点C,点P为线段OC上一点,且PA⊥PB.
如图,已知点A(0,4)、B(4,1),BC⊥x轴于点C,点P为线段OC上一点,且PA⊥PB. 解:(1)如图1所示:
解:(1)如图1所示: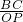 =
=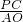 ,
,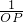 =
=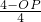 ,
,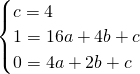 ,
,
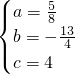 ,
, x 2-
x 2- x+4;
x+4; x 2-
x 2- x+4=
x+4= (x-
(x-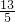 )2-
)2-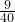 ,
, (8-
(8-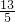 )2-
)2-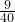 -h,
-h,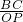 =
=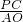 ,求出OP的长即可得出P点坐标;
,求出OP的长即可得出P点坐标;

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( ) 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设