
【题目】如图,在△ ABC中,∠ ABC、∠ ACB的平分线交于点O。
(1)若∠ABC=40°,∠ ACB=50°,则∠BOC=_______
(2)若∠ABC+∠ ACB=lO0°,则∠BOC="________"
(3)若∠A=70°,则∠BOC=_________
(4)若∠BOC=140°,则∠A=________
(5)你能发现∠ BOC与∠ A之间有什么数量关系吗?写出并说明理由。
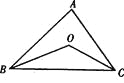
【答案】(1)、135°;(2)、130°;(3)、125°;(4)、100°;(5)、∠BOC=90°+0.5∠A
【解析】试题分析:根据角平分线的性质以及三角形内角和定理得出∠OBC和∠OCB与∠A之间的关系,然后根据△BOC的内角和定理得出∠BOC与∠A的关系.
试题解析:(1)135° (2)130° (3)125° (4)100°
(5)、BO平分∠ABC, CO平分∠ABC
∴∠OBC=0.5∠ABC ∠OCB=0.5∠ACB
∴∠OBC+∠OCB=0.5∠ABC+0.5∠ACB=
0.5(180-∠A)=90-0.5∠A
∴∠O=180-(∠OBC+∠OCB)=180-(90-0.5∠A)=90°+0.5∠A


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】图中的图形均可以由“基本图案”通过变换得到.(填序号)
(1)通过平移变换但不能通过旋转变换得到的图案是__;
(2)可以通过旋转变换但不能通过平移变换得到的图案是__;
(3)既可以由平移变换,也可以由旋转变换得到的图案是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称.其中正确的个数为 ( )
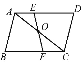
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2﹣4ac>0;④﹣ ![]() <0,正确的是( )
<0,正确的是( )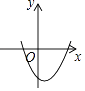
A.①②
B.②④
C.①③
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
(1)当抛物线经过点(﹣2,0)和(﹣1,3)时,求抛物线的表达式;
(2)当抛物线的顶点在直线y=﹣2x上时,求b的值;
(3)如图,现有一组这样的抛物线,它们的顶点A1、A2、…,An在直线y=﹣2x上,横坐标依次为﹣1,﹣2,﹣3,…,﹣n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1、B2 , …,Bn , 以线段AnBn为边向左作正方形AnBnCnDn , 如果这组抛物线中的某一条经过点Dn , 求此时满足条件的正方形AnBnCnDn的边长.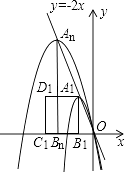
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.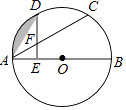
(1)求∠AFE的度数;
(2)求阴影部分的面积(结果保留π和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
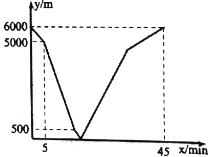
【题目】2019年3月31日,重庆举行了国际马拉松比赛,众多志愿者参与了服务工作,志愿者小茜和小悠分别从“南滨公园”和“朝天门桥”出发,沿同一条笔直的公路相向而行.小茜先出发5分钟后,小悠立刻骑自行车赶往“南滨公园”.小茜开始骑滑板车,中途改为跑步,且跑步的速度为滑板车速度的一半,到达“朝天门桥”时恰好用了45分钟.若两人之间的距离![]() 与小茜离开出发地的时间
与小茜离开出发地的时间![]() 之间的关系如图所示.则当小悠到达“南滨公园”时,小茜离“朝天门桥”的距离为__________米.
之间的关系如图所示.则当小悠到达“南滨公园”时,小茜离“朝天门桥”的距离为__________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①,图②,图③都是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图:
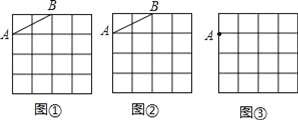
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com