练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如下图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,2),点B2019的坐标为_____

    【答案】（6058,0）

    【解析】

    首先根据已知求出三角形三边长度，然后通过旋转发现，B、B2、B4…每偶数之间的B相差6个单位长度，根据这个规律可以求得B2019的坐标．

    解：∵A（，0），B（0，2），
    ∴Rt△AOB中，AB=，
    ∴OA+AB1+B1C2=+2+=6，
    ∴B2的横坐标为：6，且B2C2=2，即B2（6，2），
    ∴B4的横坐标为：2×6=12，
    ∴点B2019的横坐标为：2018÷2×6++=6058，点B2019的纵坐标为：0，
    即B2019的坐标是（6058，0）．
    故答案为：（6058，0）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，ABCD是正方形， G是BC上（除端点外）的任意一点，DE⊥AG于点E，BF∥DE，交AG于点F．给出以下结论：①△AED≌△BFA；②DE﹣BF=EF；③△BGF∽△DAE；④DE﹣BG=FG．其中正确的有（　　）

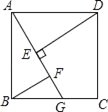
    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在四边形ABCD中，AB=AD. ∠B+∠ADC=180°，点E，F分别在四边形ABCD的边BC，CD上，∠EAF=∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系.

    图1 图2 图3

    (1)思路梳理

    将△ABE绕点A逆时针旋转至△ADG，使AB与AD重合.由∠B+∠ADC=180°，得∠FDG=180°，即点F，D，G三点共线. 易证△AFG ，故EF，BE，DF之间的数量关系为 ；

    (2)类比引申

    如图2，在图1的条件下，若点E，F由原来的位置分别变到四边形ABCD的边CB，DC的延长线上，∠EAF=∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系，并给出证明.

    (3)联想拓展

    如图3，在△ABC中，∠BAC=90°，AB=AC，点D，E均在边BC上，且∠DAE=45°. 若BD=1，EC=2，则DE的长为 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠A=30°，∠B=60°，CF平分∠ACB．

    （1）求∠ACE的度数．

    （2）若CD⊥AB于点D，∠CDF=75°，求证：△CFD是直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，已知中，厘米，、分别从点、点同时出发，沿三角形的边运动，已知点的速度是1厘米/秒的速度，点的速度是2厘米/秒，当点第一次到达点时，、同时停止运动.

    （1）、同时运动几秒后，、两点重合？

    （2）、同时运动几秒后，可得等边三角形？

    （3）、在边上运动时，能否得到以为底边的等腰，如果存在，请求出此时、运动的时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点O是线段AD的中点，分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD，连接AC和BD，相交于点E，连接BC．

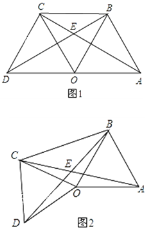
    （1）证明：⊿ABC ≌ ⊿DCB；

    （2）求∠AEB的大小．

    （3）如图2，△OAB固定不动，保持△OCD的形状和大小不变，将△OCD绕点O旋转（△OAB和△OCD不能重叠），求∠AEB的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB．添加一个条件，不能使四边形DBCE成为矩形的是（ ）

    （A）AB=BE （B）BE⊥DC （C）∠ADB=90° （D）CE⊥DE

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P是矩形ABCD的边上一动点，矩形两边长AB、BC长分别为15和20，那么P到矩形两条对角线AC和BD的距离之和是（　　）

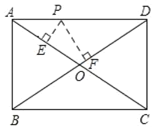
    A.6B.12C.24D.不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于三个数a，b，c，用max{a，b，c}表示这三个数中最大数，例如：max{-2，1，0}=1，max

    解决问题：

    （1）填空：max{1，2，3}=______，如果max{3，4，2x-6}=2x-6，则x的取值范围为______；

    （2）如果max{2，x+2，-3x-7}=5，求x的值；

    （3）如图，在同一坐标系中画出了三个一次函数的图象：y=-x-3，y=x-1和y=3x-3请观察这三个函数的图象，

    ①在图中画出max{-x-3，x-1，3x-3}对应的图象（加粗）；

    ②max{-x-3，x-1，3x-3}的最小值为______．

    查看答案和解析>>

    同步练习册答案