
ЎѕМвДїЎїИзНј1Ј¬ФЪЛД±ЯРОABCDЦРЈ¬AB=AD. ЎПB+ЎПADC=180ЎгЈ¬µгEЈ¬F·Ц±рФЪЛД±ЯРОABCDµД±ЯBCЈ¬CDЙПЈ¬ЎПEAF=![]() ЎПBADЈ¬Б¬ЅУEFЈ¬КФІВПлEFЈ¬BEЈ¬DFЦ®јдµДКэБї№ШПµ.
ЎПBADЈ¬Б¬ЅУEFЈ¬КФІВПлEFЈ¬BEЈ¬DFЦ®јдµДКэБї№ШПµ.

Нј1 Нј2 Нј3
(1)ЛјВ·КбАн
Ѕ«ЎчABEИЖµгAДжК±ХлРэЧЄЦБЎчADGЈ¬К№ABУлADЦШєП.УЙЎПB+ЎПADC=180ЎгЈ¬µГЎПFDG=180ЎгЈ¬јґµгFЈ¬DЈ¬GИэµг№ІПЯ. ТЧЦ¤ЎчAFG![]() Ј¬№КEFЈ¬BEЈ¬DFЦ®јдµДКэБї№ШПµОЄ Ј»
Ј¬№КEFЈ¬BEЈ¬DFЦ®јдµДКэБї№ШПµОЄ Ј»
(2)Аа±ИТэЙк
ИзНј2Ј¬ФЪНј1µДМхјюПВЈ¬ИфµгEЈ¬FУЙФАґµДО»ЦГ·Ц±р±дµЅЛД±ЯРОABCDµД±ЯCBЈ¬DCµДСУі¤ПЯЙПЈ¬ЎПEAF=![]() ЎПBADЈ¬Б¬ЅУEFЈ¬КФІВПлEFЈ¬BEЈ¬DFЦ®јдµДКэБї№ШПµЈ¬ІўёшіцЦ¤Гч.
ЎПBADЈ¬Б¬ЅУEFЈ¬КФІВПлEFЈ¬BEЈ¬DFЦ®јдµДКэБї№ШПµЈ¬ІўёшіцЦ¤Гч.
(3)БЄПлНШХ№
ИзНј3Ј¬ФЪЎчABCЦРЈ¬ЎПBAC=90ЎгЈ¬AB=ACЈ¬µгDЈ¬EѕщФЪ±ЯBCЙПЈ¬ЗТЎПDAE=45Ўг. ИфBD=1Ј¬EC=2Ј¬ФтDEµДі¤ОЄ .
Ўѕґр°ёЎїЈЁ1Ј©ЎчAFE. EF=BE+DF.ЈЁ2Ј©BF=DF-BEЈ¬АнУЙјыЅвОцЈ»ЈЁ3Ј©![]()
ЎѕЅвОцЎїКФМв·ЦОцЈєЈЁ1Ј©ПИёщѕЭРэЧЄµГЈє ![]() јЖЛг
јЖЛг![]() јґµг
јґµг![]() №ІПЯЈ¬ФЩёщѕЭSASЦ¤ГчЎчAFEЎХЎчAFGЈ¬µГEF=FGЈ¬їЙµГЅбВЫEF=DF+DG=DF+AEЈ»
№ІПЯЈ¬ФЩёщѕЭSASЦ¤ГчЎчAFEЎХЎчAFGЈ¬µГEF=FGЈ¬їЙµГЅбВЫEF=DF+DG=DF+AEЈ»
ЈЁ2Ј©ИзНј2Ј¬Н¬АнЧчёЁЦъПЯЈє°СЎчABEИЖµгAДжК±ХлРэЧЄ![]() ЦБЎчADGЈ¬Ц¤ГчЎчEAFЎХЎчGAFЈ¬µГEF=FGЈ¬ЛщТФEF=DFDG=DFBE;
ЦБЎчADGЈ¬Ц¤ГчЎчEAFЎХЎчGAFЈ¬µГEF=FGЈ¬ЛщТФEF=DFDG=DFBE;
ЈЁ3Ј©ИзНј3Ј¬Н¬АнЧчёЁЦъПЯЈє°СЎчABDИЖµгAДжК±ХлРэЧЄ![]() ЦБЎчACGЈ¬Ц¤ГчЎчAEDЎХЎчAEGЈ¬µГ
ЦБЎчACGЈ¬Ц¤ГчЎчAEDЎХЎчAEGЈ¬µГ![]() Ј¬ПИУЙ№ґ№Й¶ЁАнЗу
Ј¬ПИУЙ№ґ№Й¶ЁАнЗу![]() µДі¤Ј¬ґУ¶шµГЅбВЫЈ®
µДі¤Ј¬ґУ¶шµГЅбВЫЈ®
КФМвЅвОцЈє(1)ЛјВ·КбАнЈє
ИзНј1,°СЎчABEИЖµгAДжК±ХлРэЧЄ![]() ЦБЎчADGЈ¬їЙК№ABУлADЦШєПЈ¬јґAB=ADЈ¬
ЦБЎчADGЈ¬їЙК№ABУлADЦШєПЈ¬јґAB=ADЈ¬
УЙРэЧЄµГЈєЎПADG=ЎПA=![]() Ј¬BE=DGЈ¬ЎПDAG=ЎПBAEЈ¬AE=AGЈ¬
Ј¬BE=DGЈ¬ЎПDAG=ЎПBAEЈ¬AE=AGЈ¬
ЎаЎПFDG=ЎПADF+ЎПADG=![]() +
+![]() =
=![]() Ј¬
Ј¬
јґµгF. D.G№ІПЯЈ¬
ЎЯЛД±ЯРОABCDОЄѕШРОЈ¬
ЎаЎПBAD=![]() Ј¬
Ј¬
ЎЯЎПEAF=![]() Ј¬
Ј¬
Ўа![]()
Ўа![]()
Ўа![]()
ФЪЎчAFEєНЎчAFGЦРЈ¬
ЎЯ
ЎаЎчAFEЎХЎчAFG(SAS)Ј¬
ЎаEF=FGЈ¬
ЎаEF=DF+DG=DF+AE
№Кґр°ёОЄЈєЎчAFEЈ¬EF=DF+AEЈ»
(2)Аа±ИТэЙкЈє
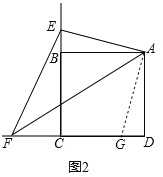
ИзНј2Ј¬EF=DFBEЈ¬АнУЙКЗЈє
°СЎчABEИЖµгAДжК±ХлРэЧЄ![]() ЦБЎчADGЈ¬їЙК№ABУлADЦШєПЈ¬ФтGФЪDCЙПЈ¬
ЦБЎчADGЈ¬їЙК№ABУлADЦШєПЈ¬ФтGФЪDCЙПЈ¬
УЙРэЧЄµГЈєBE=DGЈ¬ЎПDAG=ЎПBAEЈ¬AE=AGЈ¬
ЎЯЎПBAD=![]() Ј¬
Ј¬
ЎаЎПBAE+ЎПBAG=![]() Ј¬
Ј¬
ЎЯЎПEAF=![]() Ј¬
Ј¬
ЎаЎПFAG=![]()
![]() =
=![]() Ј¬
Ј¬
ЎаЎПEAF=ЎПFAG=![]() Ј¬
Ј¬
ФЪЎчEAFєНЎчGAFЦРЈ¬
ЎЯ
ЎаЎчEAFЎХЎчGAF(SAS)Ј¬
ЎаEF=FGЈ¬
ЎаEF=DFDG=DFBE;
(3)БЄПлНШХ№Јє
ИзНј3,°СЎчABDИЖµгAДжК±ХлРэЧЄ![]() ЦБЎчACGЈ¬їЙК№ABУлACЦШєПЈ¬Б¬ЅУEGЈ¬
ЦБЎчACGЈ¬їЙК№ABУлACЦШєПЈ¬Б¬ЅУEGЈ¬
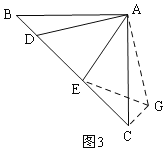
УЙРэЧЄµГЈєAD=AGЈ¬ЎПBAD=ЎПCAGЈ¬BD=CGЈ¬
ЎЯЎПBAC=![]() Ј¬AB=ACЈ¬
Ј¬AB=ACЈ¬
ЎаЎПB=ЎПACB=![]() Ј¬
Ј¬
ЎаЎПACG=ЎПB=![]() Ј¬
Ј¬
ЎаЎПBCG=ЎПACB+ЎПACG=![]() +
+![]() =
=![]() Ј¬
Ј¬
ЎЯEC=2Ј¬CG=BD=1Ј¬
УЙ№ґ№Й¶ЁАнµГЈє ![]()
ЎЯЎПBAD=ЎПCAG,ЎПBAC=
ЎаЎПDAG=![]() Ј¬
Ј¬
ЎЯЎПBAD+ЎПEAC=![]() Ј¬
Ј¬
ЎаЎПCAG+ЎПEAC=![]() =ЎПEAGЈ¬
=ЎПEAGЈ¬
ЎаЎПDAE=![]() Ј¬
Ј¬
ЎаЎПDAE=ЎПEAG=![]() Ј¬
Ј¬
ЎЯAE=AEЈ¬
ЎаЎчAEDЎХЎчAEGЈ¬
Ўа![]()


 У¦УГМвЧчТµ±ѕПµБРґр°ё
У¦УГМвЧчТµ±ѕПµБРґр°ё КојЩЧчТµКојЩїмАЦБ·Оч°Ііц°жЙзПµБРґр°ё
КојЩЧчТµКојЩїмАЦБ·Оч°Ііц°жЙзПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
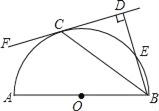
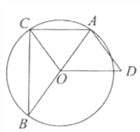
ЎѕМвДїЎїИзНјЈ¬ABКЗ°лФІOµДЦ±ѕ¶Ј¬CКЗ°лФІOЙПµДТ»µгЈ¬CFЗР°лФІOУЪµгCЈ¬BDЎНCFУЪОЄµгDЈ¬BDУл°лФІOЅ»УЪµгEЈ®
(1)ЗуЦ¤ЈєBCЖЅ·ЦЎПABDЈ®
(2)ИфDC=8Ј¬BE=4Ј¬ЗуФІµДЦ±ѕ¶Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() КЗ
КЗ![]() µДТ»МхЅЗЖЅ·ЦПЯ.µг
µДТ»МхЅЗЖЅ·ЦПЯ.µг![]() Ўў
Ўў![]() Ўў
Ўў![]() ·Ц±рФЪ
·Ц±рФЪ![]() Ўў
Ўў![]() Ўў
Ўў![]() ЙПЈ¬ЗТЛД±ЯРО
ЙПЈ¬ЗТЛД±ЯРО![]() КЗХэ·ЅРО.
КЗХэ·ЅРО.
ЈЁ1Ј©ЗуЦ¤Јєµг![]() ФЪ
ФЪ![]() µДЖЅ·ЦПЯЙПЈ»
µДЖЅ·ЦПЯЙПЈ»
ЈЁ2Ј©Иф![]() Ј¬
Ј¬![]() Ј¬ЗТХэ·ЅРО
Ј¬ЗТХэ·ЅРО![]() µДГж»эОЄ4Ј¬Зу
µДГж»эОЄ4Ј¬Зу![]() µДГж»э.
µДГж»э.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ЕЧОпПЯy=ax2+bx+cУлxЦбµДЅ»µг·Ц±рОЄAЈЁ©Ѓ6Ј¬0Ј©єНµгBЈЁ4Ј¬0Ј©Ј¬УлyЦбµДЅ»µгОЄCЈЁ0Ј¬3Ј©Ј®
ЈЁ1Ј©ЗуЕЧОпПЯµДЅвОцКЅЈ»
ЈЁ2Ј©µгPКЗПЯ¶ОOAЙПТ»¶ЇµгЈЁІ»УлµгAЦШєПЈ©Ј¬№эPЧчЖЅРРУЪyЦбµДЦ±ПЯУлACЅ»УЪµгQЈ¬µгDЎўMФЪПЯ¶ОABЙПЈ¬µгNФЪПЯ¶ОACЙПЈ®
ўЩКЗ·сН¬К±ґжФЪµгDєНµгPЈ¬К№µГЎчAPQєНЎчCDOИ«µИЈ¬ИфґжФЪЈ¬ЗуµгDµДЧш±кЈ¬ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ»
ўЪИфЎПDCB=ЎПCDBЈ¬CDКЗMNµДґ№Ц±ЖЅ·ЦПЯЈ¬ЗуµгMµДЧш±кЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
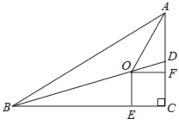
ЎѕМвДїЎїИзНјЈ¬ТСЦЄЎчABCДЪЅУУЪ![]() Ј¬ABКЗЦ±ѕ¶Ј¬ODЎОACЈ¬AD=OC.
Ј¬ABКЗЦ±ѕ¶Ј¬ODЎОACЈ¬AD=OC.
(1)ЗуЦ¤ЈєЛД±ЯРОOCADКЗЖЅРРЛД±ЯРОЈ»
(2)МоїХЈєўЩµ±ЎПB= К±Ј¬ЛД±ЯРОOCADКЗБвРОЈ»
ўЪµ±ЎПB= К±Ј¬ADУл![]() ПаЗР.
ПаЗР.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ТСЦЄЎчABCЦРЈ¬ЎПB=90 Ј¬AB=16cmЈ¬BC=12cmЈ¬PЎўQКЗЎчABC±ЯЙПµДБЅёц¶ЇµгЈ¬ЖдЦРµгPґУµгAїЄКјСШAЎъB·ЅПтФЛ¶ЇЈ¬ЗТЛЩ¶ИОЄГїГл1cmЈ¬µгQґУµгBїЄКјСШBЎъCЎъA·ЅПтФЛ¶ЇЈ¬ЗТЛЩ¶ИОЄГїГл2cmЈ¬ЛьГЗН¬К±іц·ўЈ¬Йиіц·ўµДК±јдОЄtГлЈ®
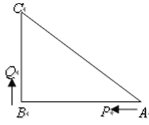
ЈЁ1Ј©іц·ў2ГлєуЈ¬ЗуPQµДі¤Ј»
ЈЁ2Ј©µ±µгQФЪ±ЯBCЙПФЛ¶ЇК±Ј¬іц·ўјёГлЦУєуЈ¬ЎчPQBДЬРОіЙµИСьИэЅЗРОЈї
ЈЁ3Ј©µ±µгQФЪ±ЯCAЙПФЛ¶ЇК±Ј¬ЗуДЬК№ЎчBCQіЙОЄµИСьИэЅЗРОµДФЛ¶ЇК±јдЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬![]() КЗ
КЗ![]() µДЦ±ѕ¶Ј¬µг
µДЦ±ѕ¶Ј¬µг![]() ФЪ
ФЪ![]() ЙПЈ¬№эµг
ЙПЈ¬№эµг![]() Чч
Чч![]() µДЗРПЯ
µДЗРПЯ![]() Ј¬СУі¤
Ј¬СУі¤![]() µЅ
µЅ![]() Ј¬К№
Ј¬К№![]() Ј¬Б¬ЅУ
Ј¬Б¬ЅУ![]() Ј¬
Ј¬![]() Ј¬Ул
Ј¬Ул![]() Ѕ»УЪµг
Ѕ»УЪµг![]() Ј®Иф
Ј®Иф![]() µД°лѕ¶ОЄ
µД°лѕ¶ОЄ![]() Ј¬
Ј¬![]() Ј¬Фт
Ј¬Фт![]() µДНвЅУФІµД°лѕ¶ОЄ________Ј®
µДНвЅУФІµД°лѕ¶ОЄ________Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзПВНј,ФЪЖЅГжЦ±ЅЗЧш±кПµЦР,Ѕ«ЎчABOИЖµгAЛіК±ХлРэЧЄµЅЎчAB1C1µДО»ЦГ,µгBЎўO·Ц±рВдФЪµгB1ЎўC1ґ¦,µгB1ФЪxЦбЙП,ФЩЅ«ЎчAB1C1ИЖµгB1ЛіК±ХлРэЧЄµЅЎчA1B1C2µДО»ЦГ,µгC2ФЪxЦбЙП,Ѕ«ЎчA1B1C2ИЖµгC2ЛіК±ХлРэЧЄµЅЎчA2B2C2µДО»ЦГ,µгA2ФЪxЦбЙП,ТАґОЅшРРПВИҐЎ.ИфµгA(![]() ,0),B(0,2),µгB2019µДЧш±кОЄ_____
,0),B(0,2),µгB2019µДЧш±кОЄ_____

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
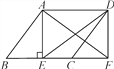
ЎѕМвДїЎїИзНјЈ¬ФЪABCDЦРЈ¬AEЎНBCУЪµгEЈ¬СУі¤BCЦБµгFК№CFЈЅBEЈ¬Б¬ЅбAFЈ¬DEЈ¬DF.
(1)ЗуЦ¤ЈєЛД±ЯРОAEFDКЗѕШРОЈ»
(2)ИфABЈЅ6Ј¬DEЈЅ8Ј¬BFЈЅ10Ј¬ЗуAEµДі¤Ј®
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com