
【题目】如图,抛物线y=ax2+bx+c与x轴的交点分别为A(﹣6,0)和点B(4,0),与y轴的交点为C(0,3).
(1)求抛物线的解析式;
(2)点P是线段OA上一动点(不与点A重合),过P作平行于y轴的直线与AC交于点Q,点D、M在线段AB上,点N在线段AC上.
①是否同时存在点D和点P,使得△APQ和△CDO全等,若存在,求点D的坐标,若不存在,请说明理由;
②若∠DCB=∠CDB,CD是MN的垂直平分线,求点M的坐标.

【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+3;(2)①点D坐标为(﹣
x+3;(2)①点D坐标为(﹣![]() ,0);②点M(
,0);②点M(![]() ,0).
,0).
【解析】
(1)应用待定系数法问题可解;
(2)①通过分类讨论研究△APQ和△CDO全等
②由已知求点D坐标,证明DN∥BC,从而得到DN为中线,问题可解.
(1)将点(-6,0),C(0,3),B(4,0)代入y=ax2+bx+c,得
 ,
,
解得: ,
,
∴抛物线解析式为:y=-![]() x2-
x2-![]() x+3;
x+3;
(2)①存在点D,使得△APQ和△CDO全等,
当D在线段OA上,∠QAP=∠DCO,AP=OC=3时,△APQ和△CDO全等,
∴tan∠QAP=tan∠DCO,
![]() ,
,
∴![]() ,
,
∴OD=![]() ,
,
∴点D坐标为(-![]() ,0).
,0).
由对称性,当点D坐标为(![]() ,0)时,
,0)时,
由点B坐标为(4,0),
此时点D(![]() ,0)在线段OB上满足条件.
,0)在线段OB上满足条件.
②∵OC=3,OB=4,
∴BC=5,
∵∠DCB=∠CDB,
∴BD=BC=5,
∴OD=BD-OB=1,
则点D坐标为(-1,0)且AD=BD=5,
连DN,CM,

则DN=DM,∠NDC=∠MDC,
∴∠NDC=∠DCB,
∴DN∥BC,
∴![]() ,
,
则点N为AC中点.
∴DN时△ABC的中位线,
∵DN=DM=![]() BC=
BC=![]() ,
,
∴OM=DM-OD=![]()
∴点M(![]() ,0)
,0)


科目:初中数学 来源: 题型:
【题目】已知:将矩形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到矩形
得到矩形![]() .
.
(1)如图![]() ,当点
,当点![]() 在
在![]() 上时,求证:
上时,求证:![]()
(2)当旋转角![]() 的度数为多少时,
的度数为多少时,![]() ?
?
(3)若![]() ,请直接写出在旋转过程中
,请直接写出在旋转过程中![]() 的面积的最大值.
的面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD是正方形, G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.给出以下结论:①△AED≌△BFA;②DE﹣BF=EF;③△BGF∽△DAE;④DE﹣BG=FG.其中正确的有( )
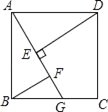
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是 ( )

A. A1(4,4),C1(3,2) B. A1(3,3),C1(2,1)
C. A1(4,3),C1(2,3) D. A1(3,4),C1(2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为![]() (分),且
(分),且![]() ,将其按分数段分为五组,绘制出以下不完整表格:
,将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩 | 频数(人数) | 频率 |
一 |
| 2 | 0.04 |
二 |
| 10 | 0.2 |
三 |
| 14 | b |
四 |
| a | 0.32 |
五 |
| 8 | 0.16 |
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有 名学生参加;
(2)直接写出表中a= ,b= ;
(3)请补全下面相应的频数分布直方图;

(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成如下不完整的条形图和扇形图.

请结合以上信息解答下列问题:
(1)m= ;
(2)请补全上面的条形统计图;
(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为 ;
(4)已知该校共有1200名学生,请你估计该校约有 名学生最喜爱足球活动.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,AB=AD. ∠B+∠ADC=180°,点E,F分别在四边形ABCD的边BC,CD上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.

图1 图2 图3
(1)思路梳理
将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合.由∠B+∠ADC=180°,得∠FDG=180°,即点F,D,G三点共线. 易证△AFG![]() ,故EF,BE,DF之间的数量关系为 ;
,故EF,BE,DF之间的数量关系为 ;
(2)类比引申
如图2,在图1的条件下,若点E,F由原来的位置分别变到四边形ABCD的边CB,DC的延长线上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°. 若BD=1,EC=2,则DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=30°,∠B=60°,CF平分∠ACB.

(1)求∠ACE的度数.
(2)若CD⊥AB于点D,∠CDF=75°,求证:△CFD是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是矩形ABCD的边上一动点,矩形两边长AB、BC长分别为15和20,那么P到矩形两条对角线AC和BD的距离之和是( )
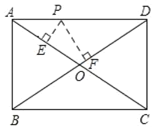
A.6B.12C.24D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com