
【题目】如图,在平面直角坐标系中,直线l:y=![]() x﹣
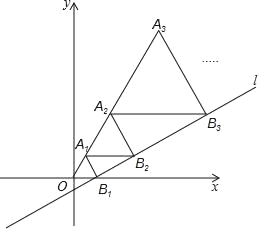
x﹣![]() 与x轴交于点B1,以OB1为一边在OB1上方作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为一边在A1B2上方作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为一边在A2B3上方作等边三角形A3A2B3,…,则△A2017B2018A2018的周长是_____.
与x轴交于点B1,以OB1为一边在OB1上方作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为一边在A1B2上方作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为一边在A2B3上方作等边三角形A3A2B3,…,则△A2017B2018A2018的周长是_____.
【答案】3×22017
【解析】分析:先根据直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,可得B1(1,0),OB1=1,△OA1B1的周长为3;再过A1作A1A⊥OB1于A,过A2作A2B⊥A1B2于B,根据等边三角形的性质以及含30°角的直角三角形的性质,分别求得A1的坐标为(
与x轴交于点B1,可得B1(1,0),OB1=1,△OA1B1的周长为3;再过A1作A1A⊥OB1于A,过A2作A2B⊥A1B2于B,根据等边三角形的性质以及含30°角的直角三角形的性质,分别求得A1的坐标为(![]() ,
,![]() ),B2(
),B2(![]() ,
,![]() ),则A1B2=2,△A1B2A2的周长是3×21,A2的坐标为(
),则A1B2=2,△A1B2A2的周长是3×21,A2的坐标为(![]() ,
,![]() ),B3(
),B3(![]() ,
,![]() ),则A2B3=4,△A2B3A3的周长是3×22,进而得到△AnBn+1An+1的周长,据此可得△A2017B2018A2018的周长.
),则A2B3=4,△A2B3A3的周长是3×22,进而得到△AnBn+1An+1的周长,据此可得△A2017B2018A2018的周长.
详解:∵直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,
与x轴交于点B1,
∴B1(1,0),OB1=1,△OA1B1的周长为3;
如图所示,过A1作A1A⊥OB1于A,

则OA=![]() OB1=
OB1=![]() ,A1A=
,A1A=![]() OA=
OA=![]() ,
,
∴A1的坐标为(![]() ,
,![]() ),
),
∵A1B2平行于x轴,
∴B2的纵坐标为![]() ,
,
将y=![]() 代入 y=
代入 y=![]() x﹣
x﹣![]() ,求得x=
,求得x=![]() ,
,
∴B2(![]() ,
,![]() ),
),
∴A1B2=2,△A1B2A2的周长是3×21;
过A2作A2B⊥A1B2于B,
则A1B=![]() A1B2=1,A2B=
A1B2=1,A2B=![]() A1B=
A1B=![]() ,
,
∴A2的横坐标为OA+A1B=![]() +1=
+1=![]() ,纵坐标为A1A+A2B=
,纵坐标为A1A+A2B=![]() ,
,
∴A2的坐标为(![]() ,
,![]() ),
),
∵A2B3平行于x轴,
∴B3的纵坐标为![]() ,
,
将y=![]() 代入y= y=
代入y= y=![]() x﹣
x﹣![]() ,求得x=
,求得x=![]() ,
,
∴B3(![]() ,
,![]() ),
),
∴A2B3=4,△A2B3A3的周长是3×22;
由此可得,△AnBn+1An+1的周长是3×2n,
∴△A2017B2018A2018的周长是3×22017.
故答案为3×22017.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,大正方形内有两个大小一样的长方形ABCD和长方形EFGH,且AB,AD,EF,EH分别在大正方形的四条边上,大正方形内有个小正方形与两长方形有重叠(图中两个长方形形状的阴影部分),若B两正方形的周长分别为44与30,且AB=EH=6,AD=EF=3,则两阴影部分的周长和为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),
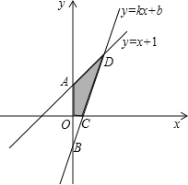
(1)求n,k ,b的值;
(2)若函数y=kx+b的函数值大于函数y=x+1的函数值,则x的取值范围是多少?
(3)求四边形AOCD的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,

求证:①△ABG≌△AFG;②BG=CG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①△ABF≌△ADF;②S△ADF=2S△CEF;③tan∠EBF=![]() ;④S△ABF=4S△BEF,其中正确结论的个数是( )
;④S△ABF=4S△BEF,其中正确结论的个数是( )
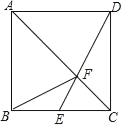
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了把巴城建成省级文明城市,特在每个红绿灯处设置了文明监督岗,文明劝导员老张某天在市中心的一十字路口,对闯红灯的人数进行统计.根据上午7:00~12:00中各时间段(以1小时为一个时间段),对闯红灯的人数制作了如图所示的扇形统计图和条形统计图,但均不完整.请你根据统计图解答下列问题:
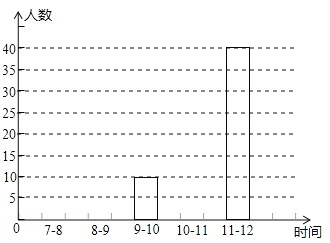

(1)问这一天上午7:00~12:00这一时间段共有多少人闯红灯?
(2)请你把条形统计图补充完整,并求出扇形统计图中9~10点,10~11点所对应的圆心角的度数.
(3)求这一天上午7:00~12:00这一时间段中,各时间段闯红灯的人数的众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进了甲、乙两种型号的中性笔共4000支,甲型号中性笔进价是3元/支,乙型号中性笔进价是7元/支,购进两种型号的中性笔共用去16000元.
(1)求甲、乙两种型号的中性笔各购进了多少支;
(2)为使每支乙型号中性笔的利润是甲型号的1.8倍,且保证售完这4000支中性笔的利润不低于7200元,求每支甲型号中性笔的售价至少是多少元.(注:利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
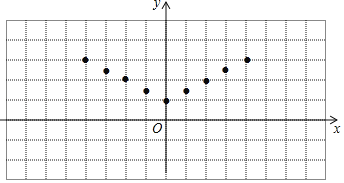
【题目】某校数学兴趣小组根据学习函数的经验,对函数y=![]() |x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
|x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
Y | … | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
(1)其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)当2<y≤3时,x的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
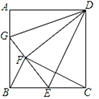
【题目】如图,已知正方形ABCD的边长为12,E是BC中点,将正方形边CD沿DE折叠到DF,将AD折叠,使AD与DF重合,折痕交AB于G,连接BF,CF,则下列结论:①G、F、E三点共线;②BG=8;③△BEF∽△CDF;④S△BFG=![]() .其中正确的有( )
.其中正确的有( )
A. ①② B. ①②③ C. ②③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com