
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,

求证:①△ABG≌△AFG;②BG=CG
【答案】①证明见解析;②证明见解析.
【解析】
①利用翻折变换对应边相等得出AB=AF,∠B=∠AFG=90°,利用HL定理得出△ABG≌△AFG即可;
②根据题意可得DE=EF=2,在Rt△ECG中,设BG=FG=x,则CG=6-x.根据勾股定理得BG=3,CG=3,从而得BG=GC.
①∵四边形ABCD是正方形,
∴AB=AD=CD=6,∠B=∠D=90°,
由折叠的性质得:∠AFE=∠D=90°,AF=AD,EF=DE,
∴∠AFG=90°,AB=AF,
∴∠B=∠AFG=90°,
在Rt△ABG和Rt△AFG中,
![]() ,
,
∴Rt△ABG≌Rt△AFG(HL);
②∵EF=DE=![]() CD=2,设BG=FG=x,则CG=6-x.
CD=2,设BG=FG=x,则CG=6-x.
在Rt△ECG中,根据勾股定理,得(6-x)2+42=(x+2)2,
解得:x=3.
∴BG=3,CG=6-3=3,
∴BG=CG.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点A,B在数轴上表示的数分别为-2与+6,动点P从点A出发,沿A→B以每秒2个单位长度的速度向终点B运动,同时,动点Q从点B出发,沿B→A以每秒4个单位长度的速度向终点A运动,当一个点到达时,另一点也随之停止运动.

(1)当Q为AB的中点时,求线段PQ的长;
(2)当Q为PB的中点时,求点P表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备购进A、B两种商品进行销售,若A种商品的进价比B种商品的进价每件少 5元,且用 90元购进A种商品的数量比用100元购进B种商品的数量多1件.
(1)求A、B两种商品的进价每件分别是多少元?
(2)若该商场购进A种商品的数量是B种商品数量的3倍少4 件,两种商品的总件数不超过96件;A种商品的销售价格为每件30元,B种商品的销售价格为每件38元,两种商品全部售出后,可使总利润超过1200元.该商场购进A、B两种商品有哪几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
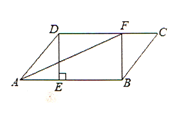
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求tan∠BAF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市民一户一表"生活用水阶梯式计费价格表的部分信息:
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
|
|
|
超过 |
|
|
超过 |
|
|
(说明:每户生产的污水量等于该户自来水用量;②水费=自来水费用+污水处理费)
已知小王家2018年7月用水![]() 吨,交水费
吨,交水费![]() 元.8月份用水
元.8月份用水![]() 吨,交水费
吨,交水费![]() 元.
元.
(1)求![]() 的值;
的值;
(2)如果小王家9月份上交水费![]() 元,则小王家这个月用水多少吨?
元,则小王家这个月用水多少吨?
(3)小王家10月份忘记了去交水费,当他11月去交水费时发现两个月一共用水50吨,其中10月份用水超过![]() 吨,一共交水费
吨,一共交水费![]() 元,其中包含
元,其中包含![]() 元滞纳金,求小王家11月份用水多少吨? (滞纳金:因未能按期缴纳水费,逾期要缴纳的“罚款金额”)
元滞纳金,求小王家11月份用水多少吨? (滞纳金:因未能按期缴纳水费,逾期要缴纳的“罚款金额”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B、C重合),CN⊥DM,CN与AB交于点N,连接OM、ON、MN.下列四个结论:①△CNB≌△DMC;②△CON≌△DOM;③AN2+CM2=MN2;④若AB=2,则S△OMN的最小值是![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
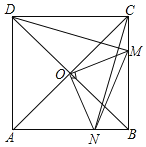
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
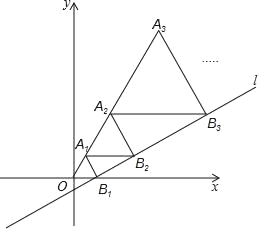
【题目】如图,在平面直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,以OB1为一边在OB1上方作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为一边在A1B2上方作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为一边在A2B3上方作等边三角形A3A2B3,…,则△A2017B2018A2018的周长是_____.
与x轴交于点B1,以OB1为一边在OB1上方作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为一边在A1B2上方作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为一边在A2B3上方作等边三角形A3A2B3,…,则△A2017B2018A2018的周长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
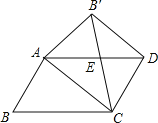
(发现与证明)ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D.
结论1:△AB′C与ABCD重叠部分的图形是等腰三角形;
结论2:B′D∥AC
…
(应用与探究)
在ABCD中,已知BC=2,∠B=45°,将△ABC沿AC翻折至△AB′C,连结B′D.若以A、C、D、B′为顶点的四边形是正方形,求AC的长.(要求画出图形)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是线段
是线段![]() 上任一点,
上任一点,![]() ,
,![]() 两点分别从
两点分别从![]() 同时向
同时向![]() 点运动,且
点运动,且![]() 点的运动速度为
点的运动速度为![]() ,
,![]() 点的运动速度为
点的运动速度为![]() ,运动的时间为
,运动的时间为![]() .
.
(1)若![]() ,
,
①运动![]() 后,求
后,求![]() 的长;
的长;
②当![]() 在线段
在线段![]() 上运动时,试说明
上运动时,试说明![]() ;
;
(2)如果![]() 时,
时,![]() ,试探索
,试探索![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com