
【题目】如图,点A,B在数轴上表示的数分别为-2与+6,动点P从点A出发,沿A→B以每秒2个单位长度的速度向终点B运动,同时,动点Q从点B出发,沿B→A以每秒4个单位长度的速度向终点A运动,当一个点到达时,另一点也随之停止运动.

(1)当Q为AB的中点时,求线段PQ的长;
(2)当Q为PB的中点时,求点P表示的数.
【答案】(1)2;(2)![]()
【解析】
(1)根据两点间的距离公式得出AB=8,根据线段中点的定义得出QB=4,根据路程除以速度等于时间得出当点Q为AB中点的时候,运动时间是1秒,此时AP=2,由PQ= AB-AP-BQ 即可算出答案;
(2) 设点P,Q的运动时间为t秒,则AP=2t,BQ=4t , PQ=AB-AP-BQ=8-6t ,根据线段中点的定义得出 PQ=BQ ,从而列出方程,求解即可.
(1)解:∵Q为AB的中点,AB=8,
OB=![]() AB=4.
AB=4.
∵点Q的运动速度为每秒4个单位长度,
∴点Q的运动时间为1秒.
∵点P的运动速度为每秒2个单位长度,
∴点P的运动路程为2个单位长度,即AP=2.
∴PQ=AB-AP-BQ=2
(2)解:设点P,Q的运动时间为t秒,则AP=2t,BQ=4t,
∴PQ=AB-AP-BQ=8-6t,
∵Q为PB的中点,
∴PQ=BQ,即8-6t=4t,
∴t=![]() ,∴AP=
,∴AP=![]() ,
,
∵![]() -2=
-2=![]() ,
,
∴点P表示的有理数是![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
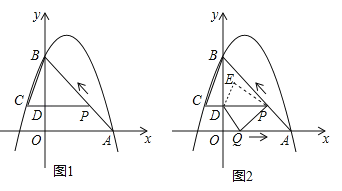
【题目】如图 1,二次函数![]() 的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接 BC ,当t=![]() 时,求△BCP的面积;
时,求△BCP的面积;
(3)如图 2,动点 P 从 A 出发时,动点 Q 同时从 O 出发,在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动,当点 P 与 B 重合时,P 、 Q 两点同时停止运动,连接 DQ 、 PQ ,将△DPQ沿直线 PC 折叠到 △DPE .在运动过程中,设 △DPE 和 △OAB重合部分的面积为 S ,直接写出 S 与 t 的函数关系式及 t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=![]() ,则称点Q为点P的“可控变点”。例如:点(1,2)的“可控变点”为点(1,2).
,则称点Q为点P的“可控变点”。例如:点(1,2)的“可控变点”为点(1,2).
结合定义,请回答下列问题:

(1)点(3,4)的“可控变点”为点 ___.
(2)若点N(m,2)是函数y=x1图象上点M的“可控变点”,则点M的坐标为___;
(3)点P为直线y=2x2上的动点,当x0时,它的“可控变点”Q所形成的图象如图所示(实线部分含实心点).请补全当x<0时,点P的“可控变点”Q所形成的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
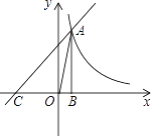
【题目】如图,在直角坐标系中,直线y=x+m与y=![]() 在第一象限交于点A,且与x轴交于点C,AB⊥x轴,垂足为B,且S△AOB=1.
在第一象限交于点A,且与x轴交于点C,AB⊥x轴,垂足为B,且S△AOB=1.
(1)求m的值;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在抛物线
在抛物线![]() 图像上,点
图像上,点![]() 在 y 轴上,若A1B0B1 、A2B1B2、…、An Bn-1Bn都为等腰直角三角形(点B0是坐标原点处),则
在 y 轴上,若A1B0B1 、A2B1B2、…、An Bn-1Bn都为等腰直角三角形(点B0是坐标原点处),则![]() 的腰长等于_____.
的腰长等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
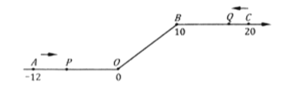
【题目】如图,将一条数轴在原点![]() 和点
和点![]() 处各折一下,得到一条“折线数轴”,图中点
处各折一下,得到一条“折线数轴”,图中点![]() 表示-12,点
表示-12,点![]() 表示10,点
表示10,点![]() 表示20,我们称点
表示20,我们称点![]() 和点
和点![]() 在数轴上相距32个长度单位.动点
在数轴上相距32个长度单位.动点![]() 从点
从点![]() 出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点
出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点![]() 运动到点
运动到点![]() 期间速度变为原来的一半,之后立刻恢复原速;同时,动点
期间速度变为原来的一半,之后立刻恢复原速;同时,动点![]() 从点
从点![]() 出发,以1单位/秒的速度沿着折线数轴的负方向运动,从点
出发,以1单位/秒的速度沿着折线数轴的负方向运动,从点![]() 运动到点
运动到点![]() 期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为
期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为![]() 秒.则:
秒.则:
(1)动点![]() 从点
从点![]() 运动至点
运动至点![]() 需要时间多少秒?
需要时间多少秒?
(2)若![]() ,
,![]() 两点在点
两点在点![]() 处相遇,则点
处相遇,则点![]() 在折线数轴上所表示的数是多少?
在折线数轴上所表示的数是多少?
(3)求当![]() 为何值时,
为何值时,![]() 、
、![]() 两点在数轴上相距的长度与
两点在数轴上相距的长度与![]() 、
、![]() 两点在数轴上相距的长度相等.
两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大正方形内有两个大小一样的长方形ABCD和长方形EFGH,且AB,AD,EF,EH分别在大正方形的四条边上,大正方形内有个小正方形与两长方形有重叠(图中两个长方形形状的阴影部分),若B两正方形的周长分别为44与30,且AB=EH=6,AD=EF=3,则两阴影部分的周长和为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,

求证:①△ABG≌△AFG;②BG=CG
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com