
【题目】如图,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,反比例函数
,反比例函数![]() 在第一象限的图象经过点B.
在第一象限的图象经过点B.
![]() 若
若![]() ,
,![]() ,则
,则![]() ______;
______;
![]() 若
若![]() 则
则![]() ______.
______.
【答案】 5 9
【解析】分析:①由![]() ,
,![]() ,可得点B的横坐标5,纵坐标1,然后把(5,1)代入
,可得点B的横坐标5,纵坐标1,然后把(5,1)代入![]() 即可求出k的值;
即可求出k的值;
②先设点B坐标(a,b),再由等腰直角三角形的性质得出OA=![]() ,AB=
,AB=![]() AD,OC=AC,AD=BD,代入OA2-AB2=18,得到ab=9,即可求得k的值.
AD,OC=AC,AD=BD,代入OA2-AB2=18,得到ab=9,即可求得k的值.
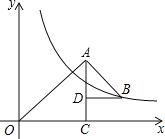
详解:①∵![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
∴OC=AC=3,AD=BD=2,
∵![]() ,
,![]() ,
,
∴点B的横坐标是OC+BD=3+2=5,纵坐标是AC-AD=3-2=1,
把(5,1)代入![]() ,得
,得
k=5;
②设点B(a,b),
∵△OAC和△BAD都是等腰直角三角形,
∴OA=![]() AC,AB=
AC,AB=![]() AD,OC=AC,AD=BD,
AD,OC=AC,AD=BD,
∵OA2AB2=18,
∴2AC22AD2=18,即AC2AD2=9
∴(AC+AD)(ACAD)=9,
∴(OC+BD) ·CD=9,
∴ab=9,
∴k=9,


科目:初中数学 来源: 题型:
【题目】2018年3月全国两会政府工作报告进一步强调“房子是用来住的,不是用来炒的”定位,继续实行差别化调控。这一年被称为史上房地产调控政策最密集、最严厉的年份。因此,房地产开发公司为了缓解年终资金周转和财务报表的压力,通常在年底大量促销。重庆某房地产开发公司一方面在“高层、洋房、别墅”三种业态的地产产品中作特价活动;另一方面,公司制定了销售刺激政策,对卖出特价的员工进行个人奖励:每卖出一套高层特价房奖励1万元,每卖出一套洋房特价房奖励2万元,每卖出一套别墅特价房奖励4万元.公司将销售人员分成三个小组,经统计,第一组平均每人售出6套高层特价房、4套洋房特价房、3套别墅特价房;第二组平均每人售出2套高层特价房、2套洋房特价房、1套别墅特价房;第三组平均每人售出8套高层特价房、5套洋房特价房。这三组销售人员在此次活动中共获得奖励466万元,其中通过销售洋房特价房所获得的奖励为216万元,且第三组销售人员的人数不超过20人。则第三组销售人员的人数比第一组销售人员的人数多___人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在数轴上表示的数分别为-2与+6,动点P从点A出发,沿A→B以每秒2个单位长度的速度向终点B运动,同时,动点Q从点B出发,沿B→A以每秒4个单位长度的速度向终点A运动,当一个点到达时,另一点也随之停止运动.

(1)当Q为AB的中点时,求线段PQ的长;
(2)当Q为PB的中点时,求点P表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
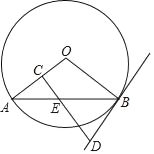
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=x+3的图象与x轴交于点A,二次函数y=x2+mx+n的图象经过点A.
(1)当m=4时,求n的值;
(2)设m=﹣2,当﹣3≤x≤0时,求二次函数y=x2+mx+n的最小值;
(3)当﹣3≤x≤0时,若二次函数﹣3≤x≤0时的最小值为﹣4,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+2S2+2S3+S4=()
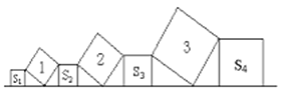
A. 5 B. 4 C. 6 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备购进A、B两种商品进行销售,若A种商品的进价比B种商品的进价每件少 5元,且用 90元购进A种商品的数量比用100元购进B种商品的数量多1件.
(1)求A、B两种商品的进价每件分别是多少元?
(2)若该商场购进A种商品的数量是B种商品数量的3倍少4 件,两种商品的总件数不超过96件;A种商品的销售价格为每件30元,B种商品的销售价格为每件38元,两种商品全部售出后,可使总利润超过1200元.该商场购进A、B两种商品有哪几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
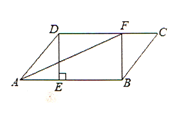
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求tan∠BAF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
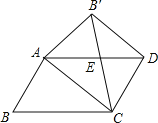
(发现与证明)ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D.
结论1:△AB′C与ABCD重叠部分的图形是等腰三角形;
结论2:B′D∥AC
…
(应用与探究)
在ABCD中,已知BC=2,∠B=45°,将△ABC沿AC翻折至△AB′C,连结B′D.若以A、C、D、B′为顶点的四边形是正方形,求AC的长.(要求画出图形)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com