练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在直线L上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4 ， 则S1+2S2+2S3+S4=（）

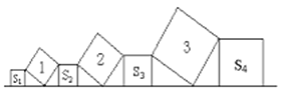
    A. 5 B. 4 C. 6 D. 10

    【答案】C

    【解析】

    试题如图，∵图中的四边形为正方形，

    ∴∠ABD=90°，AB=DB，

    ∴∠ABC+∠DBE=90°，

    ∵∠ABC+∠CAB=90°，

    ∴∠CAB=∠DBE，

    ∵在△ABC和△BDE中，

    ，

    ∴△ABC≌△BDE（AAS），

    ∴AC=BE，

    ∵DE2+BE2=BD2，

    ∴ED2+AC2=BD2，

    ∵S1=AC2，S2=DE2，BD2=1，

    ∴S1+S2=1，

    同理可得S2+S3=2，S3+S4=3，

    ∴S1+2S2+2S3+S4=1+2+3=6．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠CAB=70°，将△ABC绕点A逆时针旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′的度数是（ ）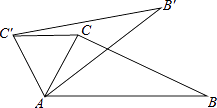
    A.70°
    B.35°
    C.40°
    D.50°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰梯形ABCD中，AD∥BC，AB=DC，AC⊥BD．若AD=4，BC=6，则梯形ABCD的面积是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是大半圆O的直径，AO是小半圆M的直径，点P是大半圆O上一点，PA与小半圆M交于点C，过点C作CD⊥OP于点D．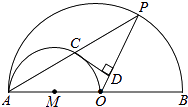
    （1）求证：CD是小半圆M的切线；
    （2）若AB=8，点P在大半圆O上运动（点P不与A，B两点重合），设PD=x，CD2=y． ①求y与x之间的函数关系式，并写出自变量x的取值范围；
    ②当y=3时，求P，M两点之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】湖州某企业新增了一个化工项目，为了节约资源，保护环境，该企业决定购买A、B两种型号的污水处理设备共10台，具体情况如下表：

    A型

    B型

    价格（万元/台）

    15

    12

    月污水处理能力（吨/月）

    250

    200

    经预算，企业最多支出136万元购买设备，且要求月处理污水能力不低于2150吨．

    （1）该企业有哪几种购买方案？

    （2）哪种方案更省钱？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一、阅读理解：

    在△ABC中，BC=a，CA=b，AB=c；

    （1）若∠C为直角，则a2+b2=c2；

    （2）若∠C为锐角，则a2+b2与c2的关系为：a2+b2＞c2；

    （3）若∠C为钝角，试推导a2+b2与c2的关系．

    二、探究问题：在△ABC中，BC=a=3，CA=b=4，AB=c，若△ABC是钝角三角形，求第三边c的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=ax2+bx+c的图象如图所示，则|a﹣b+c|+|2a+b|=（ ）
    A.a+b
    B.a﹣2b
    C.a﹣b
    D.3a

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC和△DEC中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是（　 　）

    A. BC=EC，∠B=∠E B. BC=DC，∠A=∠D

    C. BC=EC，AC=DC D. AC=DC，∠A=∠D

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点O为坐标原点，直线l与抛物线y=mx2+nx相交于A（1，3 ），B（4，0）两点．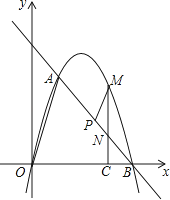
    （1）求出抛物线的解析式；
    （2）在坐标轴上是否存在点D，使得△ABD是以线段AB为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
    （3）点P是线段AB上一动点，（点P不与点A、B重合），过点P作PM∥OA，交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN ， 求出 的值，并求出此时点M的坐标．

    查看答案和解析>>

    同步练习册答案