
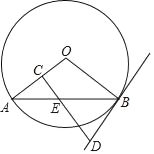
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)由切线性质及等量代换推出∠4=∠5,再利用等角对等边可得出结论;
(2)由已知条件得出sin∠DEF和sin∠AOE的值,利用对应角的三角函数值相等推出结论.
试题解析:(1)∵DC⊥OA, ∴∠1+∠3=90°, ∵BD为切线,∴OB⊥BD, ∴∠2+∠5=90°, ∵OA=OB, ∴∠1=∠2,∵∠3=∠4,∴∠4=∠5,在△DEB中, ∠4=∠5,∴DE=DB.
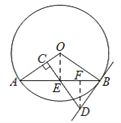
(2)作DF⊥AB于F,连接OE,∵DB=DE, ∴EF=![]() BE=3,在 RT△DEF中,EF=3,DE=BD=5,EF=3 , ∴DF=
BE=3,在 RT△DEF中,EF=3,DE=BD=5,EF=3 , ∴DF=![]() ∴sin∠DEF=
∴sin∠DEF=![]() =
= ![]() , ∵∠AOE=∠DEF, ∴在RT△AOE中,sin∠AOE=
, ∵∠AOE=∠DEF, ∴在RT△AOE中,sin∠AOE=![]() ,
,
∵AE=6, ∴AO=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,CD⊥AB于点D.P为AB延长线上一点,∠PCD=2∠BAC.
(1)求证:CP为⊙O的切线;
(2)若BP=1,CP=![]() ,求 ⊙O的半径;
,求 ⊙O的半径;

查看答案和解析>>
科目:初中数学 来源: 题型:
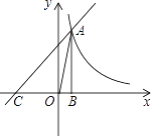
【题目】如图,在直角坐标系中,直线y=x+m与y=![]() 在第一象限交于点A,且与x轴交于点C,AB⊥x轴,垂足为B,且S△AOB=1.
在第一象限交于点A,且与x轴交于点C,AB⊥x轴,垂足为B,且S△AOB=1.
(1)求m的值;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
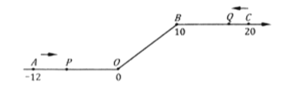
【题目】如图,将一条数轴在原点![]() 和点
和点![]() 处各折一下,得到一条“折线数轴”,图中点
处各折一下,得到一条“折线数轴”,图中点![]() 表示-12,点
表示-12,点![]() 表示10,点
表示10,点![]() 表示20,我们称点
表示20,我们称点![]() 和点
和点![]() 在数轴上相距32个长度单位.动点
在数轴上相距32个长度单位.动点![]() 从点
从点![]() 出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点
出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点![]() 运动到点
运动到点![]() 期间速度变为原来的一半,之后立刻恢复原速;同时,动点
期间速度变为原来的一半,之后立刻恢复原速;同时,动点![]() 从点
从点![]() 出发,以1单位/秒的速度沿着折线数轴的负方向运动,从点
出发,以1单位/秒的速度沿着折线数轴的负方向运动,从点![]() 运动到点
运动到点![]() 期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为
期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为![]() 秒.则:
秒.则:
(1)动点![]() 从点
从点![]() 运动至点
运动至点![]() 需要时间多少秒?
需要时间多少秒?
(2)若![]() ,
,![]() 两点在点
两点在点![]() 处相遇,则点
处相遇,则点![]() 在折线数轴上所表示的数是多少?
在折线数轴上所表示的数是多少?
(3)求当![]() 为何值时,
为何值时,![]() 、
、![]() 两点在数轴上相距的长度与
两点在数轴上相距的长度与![]() 、
、![]() 两点在数轴上相距的长度相等.
两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大正方形内有两个大小一样的长方形ABCD和长方形EFGH,且AB,AD,EF,EH分别在大正方形的四条边上,大正方形内有个小正方形与两长方形有重叠(图中两个长方形形状的阴影部分),若B两正方形的周长分别为44与30,且AB=EH=6,AD=EF=3,则两阴影部分的周长和为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB ,垂足为H,连接AC,过![]() 上一点E作 EG∥AC 交CD的延长线于点G,连接AE交CD于点F,且EG=FG .
上一点E作 EG∥AC 交CD的延长线于点G,连接AE交CD于点F,且EG=FG .
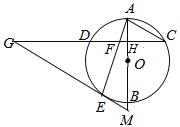
(1)求证:EG是 ⊙O 的切线;
(2)延长AB交GE的延长线于点M ,若tanG=![]() ,AH=2,求 EM 的值.
,AH=2,求 EM 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了把巴城建成省级文明城市,特在每个红绿灯处设置了文明监督岗,文明劝导员老张某天在市中心的一十字路口,对闯红灯的人数进行统计.根据上午7:00~12:00中各时间段(以1小时为一个时间段),对闯红灯的人数制作了如图所示的扇形统计图和条形统计图,但均不完整.请你根据统计图解答下列问题:
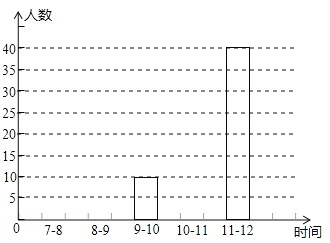

(1)问这一天上午7:00~12:00这一时间段共有多少人闯红灯?
(2)请你把条形统计图补充完整,并求出扇形统计图中9~10点,10~11点所对应的圆心角的度数.
(3)求这一天上午7:00~12:00这一时间段中,各时间段闯红灯的人数的众数和中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com