
【题目】在平面直角坐标系中,一次函数y=x+3的图象与x轴交于点A,二次函数y=x2+mx+n的图象经过点A.
(1)当m=4时,求n的值;
(2)设m=﹣2,当﹣3≤x≤0时,求二次函数y=x2+mx+n的最小值;
(3)当﹣3≤x≤0时,若二次函数﹣3≤x≤0时的最小值为﹣4,求m、n的值.
【答案】(1)3(2)-15(3)m=2,n=-3
【解析】分析:(1)根据一次函数与x轴的交点,求出A点的坐标,然后把A点坐标和m的值代入可求出n的值;
(2)表示出二次函数的对称轴,由m的值以及二次函数的图像与性质得到二次函数的最值;
(3)根据函数的对称轴的位置,分类讨论即可求出m、n的值.
详解:(1)当y=x+3=0时,x=﹣3,
∴点A的坐标为(﹣3,0).
∵二次函数y=x2+mx+n的图象经过点A,
∴0=9﹣3m+n,即n=3m﹣9,
∴当m=4时,n=3m﹣9=3.
(2)抛物线的对称轴为直线x=﹣![]() ,
,
当m=﹣2时,对称轴为x=1,n=3m﹣9=﹣15,
∴当﹣3≤x≤0时,y随x的增大而减小,
∴当x=0时,二次函数y=x2+mx+n的最小值为﹣15.
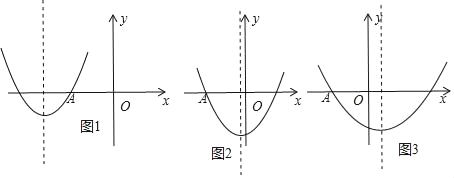
(3)①当对称轴﹣![]() ≤﹣3,即m≥6时,如图1所示.
≤﹣3,即m≥6时,如图1所示.
在﹣3≤x≤0中,y=x2+mx+n的最小值为0,
∴此情况不合题意;
②当﹣3<﹣![]() <0,即0<m<6时,如图2,
<0,即0<m<6时,如图2,
有 ,
,
解得:![]() 或
或![]() (舍去),
(舍去),
∴m=2、n=﹣3;
③当﹣![]() ≥0,即m≤0时,如图3,
≥0,即m≤0时,如图3,
有![]() ,
,
解得:![]() (舍去).
(舍去).
综上所述:m=2,n=﹣3.


科目:初中数学 来源: 题型:
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在抛物线
在抛物线![]() 图像上,点
图像上,点![]() 在 y 轴上,若A1B0B1 、A2B1B2、…、An Bn-1Bn都为等腰直角三角形(点B0是坐标原点处),则
在 y 轴上,若A1B0B1 、A2B1B2、…、An Bn-1Bn都为等腰直角三角形(点B0是坐标原点处),则![]() 的腰长等于_____.
的腰长等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大正方形内有两个大小一样的长方形ABCD和长方形EFGH,且AB,AD,EF,EH分别在大正方形的四条边上,大正方形内有个小正方形与两长方形有重叠(图中两个长方形形状的阴影部分),若B两正方形的周长分别为44与30,且AB=EH=6,AD=EF=3,则两阴影部分的周长和为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从左至右第1个图由1个正六边形,6个正方形和6个等边三角形组成;第二个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成按此规律,第![]() 个图中正方形和等边三角形的个数之和为( )
个图中正方形和等边三角形的个数之和为( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知α,β是关于x的一元二次方程x2+ (2m+3)x+m2=0 的两个不相等的实数根,且满足![]() = -1,则m的值是( ).
= -1,则m的值是( ).
A. 3或 -1 B. 3 C. -1 D. -3 或 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),
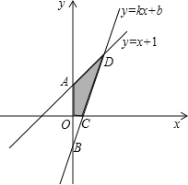
(1)求n,k ,b的值;
(2)若函数y=kx+b的函数值大于函数y=x+1的函数值,则x的取值范围是多少?
(3)求四边形AOCD的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进了甲、乙两种型号的中性笔共4000支,甲型号中性笔进价是3元/支,乙型号中性笔进价是7元/支,购进两种型号的中性笔共用去16000元.
(1)求甲、乙两种型号的中性笔各购进了多少支;
(2)为使每支乙型号中性笔的利润是甲型号的1.8倍,且保证售完这4000支中性笔的利润不低于7200元,求每支甲型号中性笔的售价至少是多少元.(注:利润=售价﹣进价)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com