
【题目】宁波某公司经销一种绿茶,每千克成本为![]() 元.市场调查发现,在一段时间内,销售量
元.市场调查发现,在一段时间内,销售量![]() (千克)随销售单价
(千克)随销售单价![]() (元/千克)的变化而变化,具体关系式为:
(元/千克)的变化而变化,具体关系式为:![]() .设这种绿茶在这段时间内的销售利润为
.设这种绿茶在这段时间内的销售利润为![]() (元),解答下列问题:
(元),解答下列问题:
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)当销售单价![]() 取何值时,销售利润
取何值时,销售利润![]() 的值最大,最大值为多少?
的值最大,最大值为多少?
(3)如果物价部门规定这种绿茶的销售单价不得高于![]() 元/千克,公司想要在这段时间内获得
元/千克,公司想要在这段时间内获得![]() 元的销售利润,销售单价应定为多少元?
元的销售利润,销售单价应定为多少元?
【答案】(1)y=-2![]() +340x-12000 ;(2)当x=85时,y的值最大,且最大值为2450;(3)当销售单价为75元时,可获得销售利润2250元.
+340x-12000 ;(2)当x=85时,y的值最大,且最大值为2450;(3)当销售单价为75元时,可获得销售利润2250元.
【解析】
(1)因为y=(x-50)w,w=-2x+240
故y与x的关系式为y=-2x2+340x-12000.
(2)用配方法化简函数式求出y的最大值即可.
(3)令y=2250时,求出x的解即可.
(1)解:由题意可知:y=(x-50)×w=(x-50)×(-2x+240)=-2![]() +340x-12000
+340x-12000
∴y 与 x 的关系式为:y=(x-50)×w=(x-50)×(-2x+240)=-2![]() +340x-12000
+340x-12000
(2)解:由(1)得:y=-2![]() +340x-12000 ,
+340x-12000 ,
配方得:y=-2![]() +2450 ;
+2450 ;
∵函数开口向下,且对称轴为x=85,
∴当x=85时,y的值最大,且最大值为2450.
(3)解:当y=2250时,可得方程 -2![]() +2450=2250;
+2450=2250;
解得:![]() =75,
=75,![]() =95 ;
=95 ;
由题意可知:x≤90,
∴![]() =95 不合题意,应该舍去。
=95 不合题意,应该舍去。
∴当销售单价为75元时,可获得销售利润2250元。


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,如果点
中,如果点![]() ,点
,点![]() 为某个菱形的一组对角的顶点,且点
为某个菱形的一组对角的顶点,且点![]() 在直线
在直线![]() 上,那么称该菱形为点
上,那么称该菱形为点![]() 的“伴随菱形”,下图为点
的“伴随菱形”,下图为点![]() 的“伴随菱形”的一个示意图.
的“伴随菱形”的一个示意图.
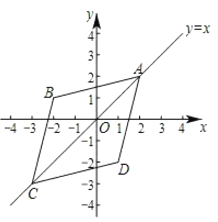
已知点![]() 的坐标为(1,1),点
的坐标为(1,1),点![]() 的坐标为
的坐标为![]() .
.
(1)点![]() 中,能够成为点
中,能够成为点![]() 的“伴随菱形”的顶点的是__________________;
的“伴随菱形”的顶点的是__________________;
(2)如果四边形![]() 是点
是点![]() 的“伴随菱形”.
的“伴随菱形”.
①当点![]() 的坐标为
的坐标为![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
②当四边形![]() 中较小内角的度数为60°时,求四边形
中较小内角的度数为60°时,求四边形![]() 的面积;
的面积;
③当四边形![]() 的面积为8,且与直线
的面积为8,且与直线![]() 有公共点时,直接写出
有公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
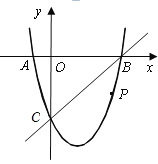
(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形![]() .是否存在点P,使四边形
.是否存在点P,使四边形![]() 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点B(6,2),C(4,0),直线y=2x+1以每秒1个单位长度的速度沿y轴向下平移,经过______秒该直线可将平行四边形OABC分成面积相等的两部分.
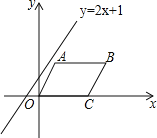
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】码头工人每天往一艘轮船上装载货物,平均每天装载速度y(吨/元)与装完货物所需时间x(天)之间是反比例函数关系,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)由于紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸货多少吨?
(3)若码头原有工人10名,且每名工人每天的装卸量相同,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?
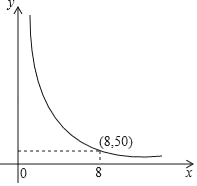
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算x[]y=![]() (其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2=
(其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2=![]() =﹣2b.已知1[]2=3,﹣1[]3=﹣2.请解答下列问题.
=﹣2b.已知1[]2=3,﹣1[]3=﹣2.请解答下列问题.
(1)求a,b的值;
(2)若M=(m2﹣m﹣1)[](2m﹣2m2),则称M是m的函数,当自变量m在﹣1≤m≤3的范围内取值时,函数值M为整数的个数记为k,求k的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,4),B(1,2),C(5,1)是平面直角坐标系中的三点.
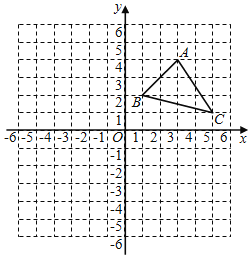
(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)分别写出点A1,B1,C1的坐标;
(3)连接AA1,BB1,求四边形AA1B1B的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com