
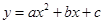 的图象与
的图象与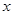 轴交于(– 1,0),(3,0);下列说法正确的是( )
轴交于(– 1,0),(3,0);下列说法正确的是( )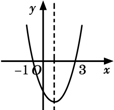
A. |
B.当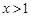 时,y随x值的增大而增大 时,y随x值的增大而增大 |
C.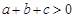 |
D.当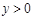 时, 时,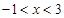 |
科目:初中数学 来源:不详 题型:解答题
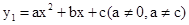 过点A(1,0),顶点为B,且抛物线不经过第三象限。
过点A(1,0),顶点为B,且抛物线不经过第三象限。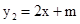 经过点B,且于该抛物线交于另一点C(
经过点B,且于该抛物线交于另一点C(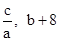 ),求当x≥1时y1的取值范围。
),求当x≥1时y1的取值范围。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).
,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).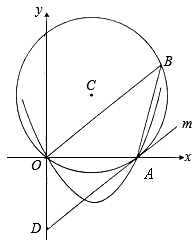
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
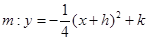 与
与 轴的交点为A、B,与
轴的交点为A、B,与 轴的交点为C,顶点为
轴的交点为C,顶点为 ,将抛物线
,将抛物线 绕点B旋转
绕点B旋转 ,得到新的抛物线
,得到新的抛物线 ,它的顶点为D.
,它的顶点为D.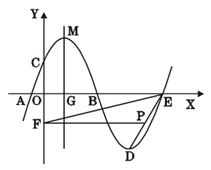
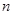 的解析式;
的解析式;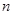 与
与 轴的另一个交点为E,点P是线段ED上一个动点(P不与E、D重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为
轴的另一个交点为E,点P是线段ED上一个动点(P不与E、D重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为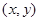 ,△PEF的面积为S,求S与
,△PEF的面积为S,求S与 的函数关系式,写出自变量
的函数关系式,写出自变量 的取值范围;
的取值范围;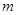 的对称轴与
的对称轴与 轴的交点为G,以G为圆心,A、B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.
轴的交点为G,以G为圆心,A、B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (克)与销售时间
(克)与销售时间 (月份)之间的函数图象. (4月份以30天计算)
(月份)之间的函数图象. (4月份以30天计算)
| 商品名称 金 额 | A | B | |||
| 投资金额x(万元) | x | 5 | x | 1 | 5 |
| 销售收入y(万元) | y1=kx (k≠0) | 3 | y2=ax2+bx(a≠0) | 2.8 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com